【题目】在平面直角坐标系xOy中,点A、B的坐标分别为(2,﹣1)、(3,0),以原点O为位似中心,把线段AB放大,点B的对应点B′的坐标为(6,0),则点A的对应点A′的坐标为 .
参考答案:
【答案】(4,﹣2)
【解析】解:∵以原点O为位似中心,B(3,0)的对应点B′的坐标为(6,0), ∴相似比为2,
∵A(2,﹣1),
∴点A′的对应点坐标为:(4,﹣2),
所以答案是:(4,﹣2).
【考点精析】根据题目的已知条件,利用位似变换的相关知识可以得到问题的答案,需要掌握它们具有相似图形的性质外还有图形的位置关系(每组对应点所在的直线都经过同一个点—位似中心).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明用尺规作图作△ABC边AC上的高BH,作法如下:
①分别以点D,E为圆心,大于 DE的长为半径作弧,两弧交于F;
DE的长为半径作弧,两弧交于F;
②作射线BF,交边AC于点H;
③以B为圆心,BK长为半径作弧,交直线AC于点D和E;
④取一点K,使K和B在AC的两侧;
所以,BH就是所求作的高.其中顺序正确的作图步骤是( )
A.①②③④
B.④③②①
C.②④③①
D.④③①② -
科目: 来源: 题型:
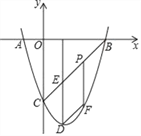
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴相交于A、B两点,点B的坐标为(3,0),与y轴相交于点C(0,﹣3),顶点为D.
(1)求出抛物线y=x2+bx+c的表达式;
(2)连结BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.
①当m为何值时,四边形PEDF为平行四边形.
②设四边形OBFC的面积为S,求S的最大值.
-
科目: 来源: 题型:
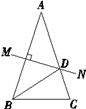
查看答案和解析>>【题目】如图,△ABC中,∠A=40°,AB的垂直平分线MN交AC于点D,∠DBC=30°,若AB=m,BC=n,则△DBC的周长为( )
A.m+n
B.2m+n
C.m+2n
D.2m -n -
科目: 来源: 题型:
查看答案和解析>>【题目】将△ABC的各个顶点的横坐标分别加3,纵坐标不变,连接三个新的点所成的三角形是由△ABC()
A.向左平移3个单位所得 B.向右平移3个单位所得
C.向上平移3个单位所得 D.向下平移3个单位所得
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国最新研制的巨型计算机“曙光3000超级服务器”,它的运算峰值可以达到每秒403200000000次,403200000000用科学记数法来表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
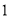 ,二次函数
,二次函数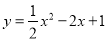 的图象与一次函数
的图象与一次函数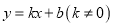 的图象交于
的图象交于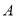 ,
, 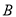 两点,点
两点,点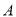 的坐标为
的坐标为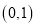 ,点
,点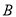 在第一象限内,点
在第一象限内,点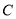 是二次函数图象的顶点,点
是二次函数图象的顶点,点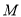 是一次函数
是一次函数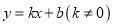 的图象与
的图象与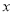 轴的交点,过点
轴的交点,过点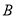 作
作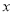 轴的垂线,垂足为
轴的垂线,垂足为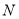 ,且
,且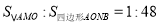 .
. (
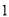 )求直线
)求直线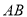 和直线
和直线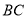 的解析式.
的解析式.(2)点
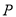 是线段
是线段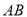 上一点,点
上一点,点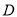 是线段
是线段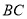 上一点,
上一点, 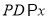 轴,射线
轴,射线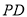 与抛物线交于点
与抛物线交于点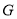 ,过点
,过点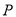 作
作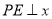 轴于点
轴于点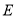 ,
, 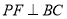 于点
于点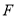 ,当
,当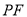 与
与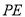 的乘积最大时,在线段
的乘积最大时,在线段 上找一点
上找一点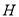 (不与点
(不与点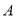 ,点
,点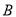 重合),使
重合),使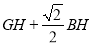 的值最小,求点
的值最小,求点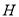 的坐标和
的坐标和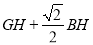 的最小值.
的最小值.(
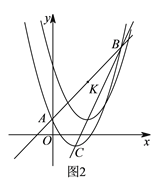
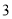 )如图
)如图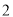 ,直线
,直线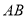 上有一点
上有一点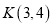 ,将二次函数
,将二次函数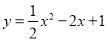 沿直线
沿直线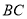 平移,平移的距离是
平移,平移的距离是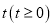 ,平移后抛物线使点
,平移后抛物线使点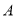 ,点
,点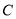 的对应点分别为点
的对应点分别为点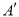 ,点
,点 ;当
;当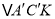 是直角三角形时,求t的值.
是直角三角形时,求t的值.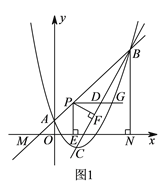
相关试题

