【题目】如图,在△ABC中,∠C=90°,点P是斜边AB的中点,点M从点C向点A匀速运动,点N从点B向点C匀速运动,已知两点同时出发,同时到达终点,连接PM、PN、MN,在整个运动过程中,△PMN的面积S与运动时间t的函数关系图象大致是( )
A.
B.
C.
D.
参考答案:
【答案】A
【解析】如图1,连接CP,∵点P是斜边AB的中点,∴S△ACP=S△BCP=![]() S△ABC , 出发时,S△PMN=S△BCP=
S△ABC , 出发时,S△PMN=S△BCP=![]() S△ABC;∵两点同时出发,同时到达终点,
S△ABC;∵两点同时出发,同时到达终点,
∴点N到达BC的中点时,点M也到达AC的中点,∴S△PMN=![]() S△ABC;结束时,S△PMN=S△ACP=
S△ABC;结束时,S△PMN=S△ACP=![]() S△ABC , 在整个运动过程中设BC=a,AC=b,
S△ABC , 在整个运动过程中设BC=a,AC=b,
∴S= ![]() [ab﹣VNt
[ab﹣VNt![]() -(a﹣VNt)VMt-(b﹣VMt)
-(a﹣VNt)VMt-(b﹣VMt)![]() ]=
]= ![]() (ab﹣
(ab﹣![]() VNbt﹣aVMt+ VNVMt2﹣
VNbt﹣aVMt+ VNVMt2﹣![]() ab+
ab+![]() aVMt)=
aVMt)= ![]() VNVMt2﹣
VNVMt2﹣![]() (VNb+aVM)t+
(VNb+aVM)t+![]() ab,∴△MPQ的面积大小变化情况是:先减小后增大,而且是以抛物线的方式变化,∴△PMN的面积S与运动时间t的函数关系图象大致是:
ab,∴△MPQ的面积大小变化情况是:先减小后增大,而且是以抛物线的方式变化,∴△PMN的面积S与运动时间t的函数关系图象大致是: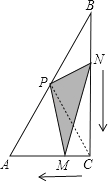
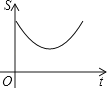 . 故选:A.
. 故选:A.
【考点精析】通过灵活运用函数的图象,掌握函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图案中既是轴对称图形,又是中心对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )

A.10cm
B.8cm
C.6cm
D.4cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线AB与x轴交于点A(﹣2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线y=
 (k≠0)上,则k的值为( )
(k≠0)上,则k的值为( )
A.4
B.-2
C.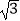
D.-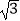
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为开拓学生视野,开展“课外读书周”活动,活动后期随机调查了九年级部分学生一周的课外阅读时间,并将结果绘制成两幅不完整的统计图,请你根据统计图的信息回答下列问题:

(1)本次调查的学生总数为____人,被调查学生的课外阅读时间的中位数是___小时,众数是___小时;
(2)请你补全条形统计图;
(3)在扇形统计图中,课外阅读时间为5小时的扇形的圆心角度数是;
(4)若全校九年级共有学生700人,估计九年级一周课外阅读时间为6小时的学生有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】张老师利用休息时间组织学生测量山坡上一棵大树CD的高度,如图,山坡与水平面成30°角(即∠MAN=30°),在山坡底部A处测得大树顶端点C的仰角为45°,沿坡面前进20米,到达B处,又测得树顶端点C的仰角为60°(图中各点均在同一平面内),求这棵大树CD的高度(结果精确到0.1米,参考数据:
 ≈1.732)
≈1.732)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D是等边△ABC中BC边的延长线上一点,且AC=CD,以AB为直径作⊙O,分别交边AC、BC于点E、点F

(1)求证:AD是⊙O的切线;
(2)连接OC,交⊙O于点G,若AB=4,求线段CE、CG与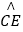 围成的阴影部分的面积S.
围成的阴影部分的面积S.
相关试题

