【题目】如图1,在等边△ABC的边AC的延长线上取一点E,以CE为边作等边△CDE,使它与△ABC位于直线AE的同侧. 
(1)同学们对图1进行了热烈的讨论,猜想出如下结论,你认为正确的有(填序号). ①△ACD≌△BCE;②△ACP≌△BCQ; ③△DCP≌△ECQ;④∠ARB=60°;⑤△CPQ是等边三角形.
(2)当等边△CED绕C点旋转一定角度后(如图2),(1)中有哪些结论还是成立的?并对正确的结论分别予以证明. 
参考答案:
【答案】
(1)①②③④⑤
(2)解:当等边△CED绕C点旋转一定角度后 (1)中结论①、④仍然成立,证明如下:
∵△ABC和△CDE是等边三角形
∴CA=CB,CD=CE,∠ACB=∠ECD=60°,
∴∠ACB+∠BCD=∠ECD+∠BCD
即∠ACD=∠BCE,
在△ACD和△BCE中,
 ,
,
∴△ACD≌△BCE(SAS),
∴∠BCE=∠CAD,
又∵∠APC=∠BPR,
∴∠ACB=∠ARB,
∵∠ACB=60°,
∴∠ARB=60°.
【解析】解:(1)∵等边△ABC和等边△CDE, ∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD=∠BCE,
在△ACD与△BCE中, ,
,
∴△ACD≌△BCE(SAS),
∴∠DAC=∠EBC,
同理证明△ACP≌△BCQ;△DCP≌△ECQ;
进而得出∠ARB=60°;△CPQ是等边三角形;
所以正确的有①②③④⑤;
故答案为:①②③④⑤;
(1)根据等边三角形的性质得出各角都是60°,各边相等,再利用全等三角形的判定和性质证明即可;(2)根据旋转的性质和全等三角形的判定解答即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列性质中菱形不一定具有的性质是( )
A. 对角线互相平分 B. 对角线相等
C. 对角线互相垂直 D. 既是轴对称图形又是中心对称图形
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个长方体模型,它的长为8×103cm,宽为5×102cm,高为3×102cm,它的体积是多少cm3?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列判断中正确的是( )
A.对角线互相垂直的四边形是菱形
B.三个角相等的四边形是矩形
C.对角线相等的平行四边形是正方形
D.对角线互相平分垂直且相等的四边形是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】4的算术平方根是_____,﹣64的立方根是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正比例函数y=x与反比例函数y=
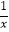 的图像交于点A、点C,AB⊥x轴于点B,CD⊥x轴于点D,则四边形ABCD的面积为 .
的图像交于点A、点C,AB⊥x轴于点B,CD⊥x轴于点D,则四边形ABCD的面积为 . 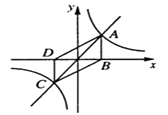
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x(x+5)=x+5的解为_____.
相关试题

