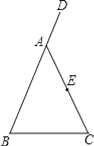
【题目】如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点.
(1)利用尺规作出∠DAC的平分线AM,连接BE并延长交AM于点F,(要求在图中标明相应字母,保留作图痕迹,不写作法);
(2)试判断AF与BC有怎样的位置关系与数量关系,并说明理由.
参考答案:
【答案】(1)作图见解析;(2)AF∥BC且AF=BC,理由见解析.
【解析】试题分析:(1)根据题意画出图形即可;
(2)根据等腰三角形的性质,可得两底角相等,根据三角形的外角的性质,可得∠DAC=∠ABC+∠C,根据内错角相等,可得两直线平行,根据ASA,可得两个三角形全等,根据全等三角形的性质,可得证明结论.
试题解析:(1)如图:
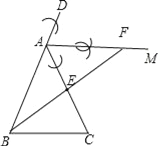
(2)AF∥BC且AF=BC,理由如下:
∵AB=AC,∴∠ABC=∠C,
∵∠DAC=∠ABC+∠C,∴∠DAC=2∠C,
由作图可知∠DAC=2∠FAC,∴∠C=∠FAC,∴AF∥BC;
∵E是AC的中点,∴AE=CE,
在△AEF和△CEB中, 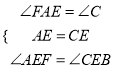 ,∴△AEF≌△CEB (ASA),
,∴△AEF≌△CEB (ASA),
∴AF=BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小晗家客厅装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,在正常情况下,小晗按下任意一个开关均可打开对应的一盏电灯,既可三盏、两盏齐开,也可分别单盏开.因刚搬进新房不久,不熟悉情况.
(1)若小晗任意按下一个开关,正好楼梯灯亮的概率是多少?
(2)若任意按下一个开关后,再按下另两个开关中的一个,则正好客厅灯和走廊灯同时亮的概率是多少?请用树状图或列表法加以说明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、ED分别垂直于BD,点B、D是垂足,且∠ACB=∠CED.求证:△ACE是直角三角形

-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学报名参加校运动会,有以下5个项目可供选择:
径赛项目:100m,200m,400m(分别用A1、A2、A3表示);
田赛项目:跳远,跳高(分别用B1、B2表示).
(1)该同学从5个项目中任选一个,恰好是田赛项目的概率为________;
(2)该同学从5个项目中任选两个,利用树状图或列表列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把四块长为a,宽为b的长方形木板围成如图所示的正方形,请解答下列问题:
(1)按要求用含a,b的式子表示空心部分的正方形的面积S(结果不要化简,保留原式):
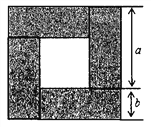
①用大正方形面积减去四块木板的面积表示:S= ;
②直接用空心部分的正方形边长的平方表示:S= ;
(2)由①、②可得等式 ;
(3)用整式的乘法验证(2)中的等式成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一条直线上有两只蚂蚁,甲蚂蚁在点A处,乙蚂蚁在点B处,假设两只蚂蚁同时出发,爬行方向只能沿直线AB在“向左”或“向右”中随机选择,并且甲蚂蚁爬行的速度比乙蚂蚁快.(1)甲蚂蚁选择“向左”爬行的概率为________;
(2)利用列表或画树状图的方法求两只蚂蚁开始爬行后会“触碰到”的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的内容,再解决问题.
例题:若
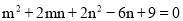 , 求m和n的值
, 求m和n的值解:∵
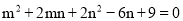
∴
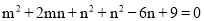
∴
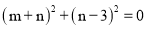
∴
 ,
, 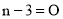
∴
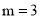 ,
, 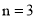
问题:(1)若
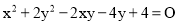 ,求
,求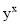 的值.
的值.(2)已知a,b,c是△ABC的三边长,满足
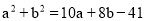 ,且c是△ABC中最长的边,求c的取值范围.
,且c是△ABC中最长的边,求c的取值范围.
相关试题

