搜索
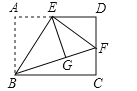
【题目】如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F. 若AB=6,BC=
,则FD的长为( )
A. 2B. 4C. 6D. 23
参考答案：
【答案】B
【解析】
根据点E是AD的中点以及翻折的性质可以求出AE=DE=EG，然后利用“HL”证明△EDF和△EGF全等，根据全等三角形对应边相等可证得DF=GF；设FD=x，表示出FC、BF，然后在Rt△BCF中，利用勾股定理列式进行计算即可得解．
∵E是AD的中点，
∴AE=DE，
∵△ABE沿BE折叠后得到△GBE，
∴AE=EG，AB=BG，
∴ED=EG，
∵在矩形ABCD中，
∴∠A=∠D=90°，
∴∠EGF=90°，
∵在Rt△EDF和Rt△EGF中，
，
∴Rt△EDF≌Rt△EGF(HL)，
∴DF=FG，
设DF=x，则BF=6+x，CF=6-x，
在Rt△BCF中，(4
)2+(6-x)2=(6+x)2，
解得x=4，
故选B．
-
科目： 来源： 题型：
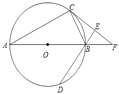
查看答案和解析>>【题目】如图，AB为⊙O的直径，C、D为⊙O上不同于A、B的两点，∠ABD=2∠BAC，过点C作CE⊥DB交DB的延长线于点E，直线AB与CE相交于点F．
（1）求证：CF为⊙O的切线；
（2）填空：当∠CAB的度数为________时，四边形ACFD是菱形．
【答案】30°
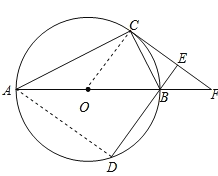
【解析】（1）连结OC，如图，由于∠A=∠OCA，则根据三角形外角性质得∠BOC=2∠A，而∠ABD=2∠BAC，所以∠ABD=∠BOC，根据平行线的判定得到OC∥BD，再CE⊥BD得到OC⊥CE，然后根据切线的判定定理得CF为⊙O的切线；
（2）根据三角形的内角和得到∠F=30°，根据等腰三角形的性质得到AC=CF，连接AD，根据平行线的性质得到∠DAF=∠F=30°，根据全等三角形的性质得到AD=AC，由菱形的判定定理即可得到结论．答：
(1)证明：连结OC，如图，
∵OA=OC，
∴∠A=∠OCA，
∴∠BOC=∠A+∠OCA=2∠A，
∵∠ABD=2∠BAC，
∴∠ABD=∠BOC，
∴OC∥BD，
∵CE⊥BD，
∴OC⊥CE，
∴CF为⊙O的切线;
(2)当∠CAB的度数为30°时，四边形ACFD是菱形，理由如下：
∵∠A=30°，
∴∠COF=60°，
∴∠F=30°，
∴∠A=∠F，
∴AC=CF，
连接AD，
∵AB是⊙O的直径，
∴AD⊥BD，
∴AD∥CF，
∴∠DAF=∠F=30°，
在△ACB与△ADB中,
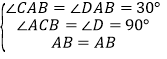，∴△ACB≌△ADB，
∴AD=AC，
∴AD=CF，
∵AD∥CF，
∴四边形ACFD是菱形。
故答案为：30°.
【题型】解答题
【结束】
22【题目】经市场调查，某种商品在第x天的售价与销量的相关信息如下表；已知该商品的进价为每件30元，设销售该商品每天的利润为y元．
（1）求出y与x的函数关系式
（2）问销售该商品第几天时，当天销售利润最大？最大利润是多少？
（3）该商品销售过程中，共有多少天日销售利润不低于4800元？直接写出答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若化简|1-x|-
的结果为2x﹣5，则x的取值范围是（ ）A. x为任意实数B. 1≤x≤4 C. x≥1D. x≤4
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图在Rt△ABC中，∠BAC=90°，AD是斜边BC上的高，BE为∠ABC的角平分线交AC于E，交AD于F，FG∥BD，交AC于G，过E作EH⊥CD于H，连接FH，下列结论：①四边形CHFG是平行四边形，②AE=CG，③FE=FD，④四边形AFHE是菱形，其中正确的是（ ）
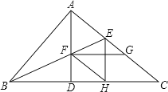
A．①②③④ B．②③④ C．①③④ D．①②④
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校兴趣小组想测量一座大楼AB的高度．如图6，大楼前有一段斜坡BC，已知BC的长为12米，它的坡度i=1：
．在离C点40米的D处，用测角仪测得大楼顶端A的仰角为37°，测角仪DE的高为1.5米，求大楼AB的高度约为多少米？（结果精确到0.1米）（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，
≈1.73．）
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校兴趣小组想测量一座大楼AB的高度．如图6，大楼前有一段斜坡BC，已知BC的长为12米，它的坡度i=1：
．在离C点40米的D处，用测角仪测得大楼顶端A的仰角为37°，测角仪DE的高为1.5米，求大楼AB的高度约为多少米？（结果精确到0.1米）（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，
≈1.73．）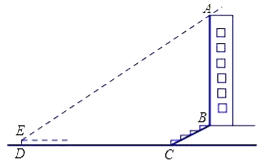
【答案】33.3．
【解析】
试题分析：延长AB交直线DC于点F，过点E作EH⊥AF，垂足为点H，在Rt△BCF中利用坡度的定义求得CF的长，则DF即可求得，然后在直角△AEH中利用三角函数求得AF的长，进而求得AB的长．
试题解析：延长AB交直线DC于点F，过点E作EH⊥AF，垂足为点H．
∵在Rt△BCF中，
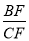=i=1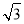：，∴设BF=k，则CF=
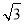k，BC=2k．又∵BC=12，∴k=6，∴BF=6，CF=
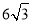．∵DF=DC+CF，∴DF=40+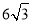．∵在Rt△AEH中，tan∠AEH=
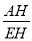，∴AH=tan37°×（40+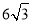）≈37.8（米），∵BH=BF﹣FH，∴BH=6﹣1.5=4.5．∵AB=AH﹣HB，∴AB=37.8﹣4.5=33.3．答：大楼AB的高度约为33.3米．
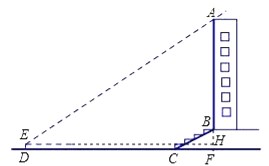
考点：1．解直角三角形的应用-仰角俯角问题；2．解直角三角形的应用-坡度坡角问题．
【题型】解答题
【结束】
24【题目】为迎接安顺市文明城市创建工作，某校八年一班开展了“社会主义核心价值观、未成年人基本文明礼仪规范”的知识竞赛活动，成绩分为A、B、C、D四个等级，并将收集的数据绘制了两幅不完整的统计图.请你根据图中所给出的信息，解答下列各题:
(1)求八年一班共有多少人；
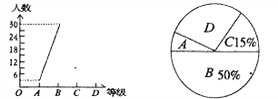
(2)补全折线统计图；
(3)在扇形统计图中等极为“D”的部分所占圆心角的度数为________；
(4)若等级A为优秀，求该班的优秀率.
-
科目： 来源： 题型：
查看答案和解析>>【题目】Rt△ABC中，∠BAC=90°，AB=3，AC=4，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值为______．
相关试题
