【题目】某企业对每个员工在当月生产某种产品的件数统计如下:设产品件数为x(单位:件),企业规定:当x<15时为不称职;当15≤x<20时为基本称职;当20≤x<25为称职;当x≥25时为优秀.解答下列问题
(1)试求出优秀员工人数所占百分比;
(2)计算所有优秀和称职的员工中月产品件数的中位数和众数;
(3)为了调动员工的工作积极性,企业决定制定月产品件数奖励标准,凡达到或超过这个标准的员工将受到奖励.如果要使得所有优秀和称职的员工中至少有一半能获奖,你认为这个奖励标准应定为多少件合适?简述其理由.
参考答案:
【答案】
(1)解:根据条形图可以得出:优秀营业员人数为3人,总人数为:30人,
则优秀营业员人数所占百分比: ![]() ×100%=10%
×100%=10%
(2)解:∵所有优秀和称职的营业员为21人,最中间的是第11个数据,第11个数据为22,
∴中位数为:22,
∵20出现次数最多,∴众数为:20;
故所有优秀和称职的营业员中月销售件数的中位数22、众数20.
(3)解:奖励标准应定为22件.中位数是一个位置代表值,它处于这组数据的中间位置,
因此大于或等于中位数的数据至少有一半.所以奖励标准应定为22件.
【解析】(1)根据条形图可以得出优秀营业员人数和总人数,从而求解;
(2)根据中位数和众数的定义可解答;众数是出现次数最多的数;把一组数据从小到大排列,处于中间的数和中间两个数的平均数叫中位数.
(3)可根据中位数的意义来解答.中位数是一个位置代表值,它处于这组数据的中间位置.
【考点精析】掌握条形统计图和中位数、众数是解答本题的根本,需要知道能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况;中位数是唯一的,仅与数据的排列位置有关,它不能充分利用所有数据;众数可能一个,也可能多个,它一定是这组数据中的数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点的三角形叫做格点三角形.
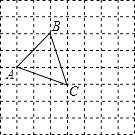
(1)格点△ABC的面积为;
(2)画出格点△ABC绕点C顺时针旋转90°后的△A1B1C1 , 并求出在旋转过程中,点B所经过的路径长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
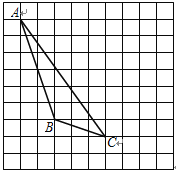
(1)画出△ABC向右平移4个单位后得到的△A1B1C1;
(2)图中AC与A1C1的关系是: _____________.
(3)画出△ABC的AB边上的高CD;垂足是D;
(4)图中△ABC的面积是_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD的四边都相等,等边△AEF的顶点E、F分别在BC、CD上,且AE=AB,则∠C=( )

A. 100° B. 105° C. 110° D. 120°
-
科目: 来源: 题型:
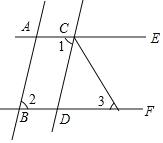
查看答案和解析>>【题目】如图,已知AB∥CD,∠1=∠2,CF平分∠DCE.
(1)试判断直线AC与BD有怎样的位置关系?并说明理由;
(2)若∠1=80°,求∠3的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,∠AOB:∠BOC=5:3,OD是∠BOC的平分线,OE是∠AOC的平分线,且∠BOE=16°,求∠DOE的度数.

-
科目: 来源: 题型:
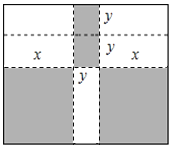
查看答案和解析>>【题目】如图,将一张长方形大铁皮切割成九块,切痕如图虚线所示,其中有两块是边长都为xdm的大正方形,两块是边长都为ydm的小正方形,五块是长宽分别是xdm、ydm的全等小长方形,且x>y.
(1)用含x、y的代数式表示长方形大铁皮的周长为______dm;
(2)若每块小长方形的面积10dm2,四个正方形的面积为58dm2,试求该切痕的总长.
相关试题

