搜索
【题目】某校九年级数学兴趣小组的同学进行社会实践活动时，想利用所学的解直角三角形的知识测量某塔的高度，他们先在点
用高
米的测角仪
测得塔顶
的仰角为
，然后沿
方向前行
m到达点
处，在
处测得塔顶
的仰角为
．请根据他们的测量数据求此塔
的高．（结果精确到
m，参考数据： 
， 
， 
）
参考答案：
【答案】36.1．
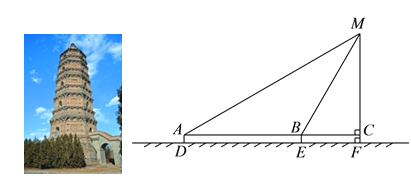
【解析】试题分析：首先证明AB=BM=40，在Rt△BCM中，利用勾股定理求出CM即可解决问题；
试题解析：解：由题意：AB=40，CF=1.5．∵∠MAC=30°，∠MBC=60°，∴∠AMB=30°，∴∠AMB=∠MAB，∴AB=MB=40．在Rt△BCM中，∵∠MCB=90°，∠MBC=60°，∴∠BMC=30°，∴BC=
BM=20，∴MC=
=
，∴MC≈34.64，∴MF=CF+CM=36.14≈36.1．
-
科目： 来源： 题型：
查看答案和解析>>【题目】求若干个相同的不为零的有理数的除法运算叫做除方.
如：2÷2÷2，(-3)÷(-3)÷(-3 )÷( -3)等. 类比有理数的乘方，我们把 2÷2÷2 记作 2③，读作“2 的圈 3 次方”. (-3)÷(-3)÷(-3 )÷( -3)记作(-3)④，读作“-3 的圈 4 次方”.
一般地，把
（a≠0）记作
，读作“a的圈n次方”.(1)直接写出计算结果：
_____， 
_________， 
___________，(2)我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，
请尝试将有理数的除方运算转化为乘方运算，归纳如下：一个非零有理数的圈 n 次方等于_____.
(3)计算
. -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，点A（t﹣1，1）与点B关于过点（t，0）且垂直于x轴的直线对称．
（1）以AB为底边作等腰三角形ABC，
①当t＝2时，点B的坐标为 ；
②当t＝0.5且直线AC经过原点O时，点C与x轴的距离为 ；
③若
上所有点到y轴的距离都不小于1，则t的取值范围是 ．（2）以AB为斜边作等腰直角三角形ABD，直线m过点（0，b）且与x轴平行，若直线m上存在点P，
上存在点K，满足PK＝1，直接写出b的取值范围． -
科目： 来源： 题型：
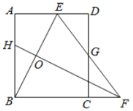
查看答案和解析>>【题目】如图，矩形ABCD中，AB＝12，点E是AD上的一点，AE＝6，BE的垂直平分线交BC的延长线于点F，连接EF交CD于点G．若G是CD的中点，则BC的长是__________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，是一座古拱桥的截面图，拱桥桥洞的上沿是抛物线形状，当水面的宽度为10m时，桥洞与水面
的最大距离是5m．
（1）经过讨论，同学们得出三种建立平面直角坐标系的方案（如下图）
你选择的方案是_____（填方案一，方案二，或方案三），则B点坐标是______，求出你所选方案中的抛物线的表达式；
（2）因为上游水库泄洪，水面宽度变为6m，求水面上涨的高度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】【背景知识】数轴是初中数学的一个重要工具，利用数轴可以将数与形完美地结 合.研究数轴我们发现了许多重要的规律：若数轴上点 A、点 B 表示的数分别为 a、b，则A、B 两点之间的距离 AB=
，线段 AB 的中点表示的数为
.【问题情境】如图，数轴上点A表示的数为-2，点B表示的数为8，点P从点 A 出发， 以每秒3个单位长度的速度沿数轴向右匀速运动，同时点Q从点B出发，以每秒 2个单 位长度的速度向左匀速运动，设运动时间为t秒(t＞0).
【综合运用】(1) 填空：
①A、B两点之间的距离AB=__________，线段AB的中点表示的数为_______；
②用含t的代数式表示：t秒后，点P表示的数为_______；点Q表示的数为_____.
(2) 求当t为何值时，P、Q 两点相遇，并写出相遇点所表示的数；
(3)求当t为何值时，PQ=
AB；(4)若点M为PA的中点，点N为PB的中点，点 P在运动过程中，线段MN的长度是否发 生变化？若变化，请说明理由；若不变，请求出线段MN的长.
-
科目： 来源： 题型：
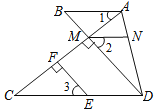
查看答案和解析>>【题目】如图，已知：EF⊥AC，垂足为点F，DM⊥AC，垂足为点M，DM的延长线交AB于点B，且∠1＝∠C，点N在AD上，且∠2＝∠3，试说明AB∥MN.
相关试题
