【题目】在平面直角坐标系xOy中,点A(t﹣1,1)与点B关于过点(t,0)且垂直于x轴的直线对称.
(1)以AB为底边作等腰三角形ABC,
①当t=2时,点B的坐标为 ;
②当t=0.5且直线AC经过原点O时,点C与x轴的距离为 ;
③若![]() 上所有点到y轴的距离都不小于1,则t的取值范围是 .
上所有点到y轴的距离都不小于1,则t的取值范围是 .
(2)以AB为斜边作等腰直角三角形ABD,直线m过点(0,b)且与x轴平行,若直线m上存在点P,![]() 上存在点K,满足PK=1,直接写出b的取值范围.
上存在点K,满足PK=1,直接写出b的取值范围.
参考答案:
【答案】(1)①(3,1);② 1;③ ![]() 或
或![]() ;(2)当点D在AB上方时,若直线m上存在点P,
;(2)当点D在AB上方时,若直线m上存在点P,![]() 上存在点K,满足PK=1,则
上存在点K,满足PK=1,则![]() ;当点D在AB下方时,若直线m上存在点P,
;当点D在AB下方时,若直线m上存在点P,![]() 上存在点K,满足PK=1,则
上存在点K,满足PK=1,则![]() .或
.或![]()
【解析】
(1)①根据A,B关于直线x=2对称解决问题即可.
②求出直线OA与直线x=0.5的交点C的坐标即可判断.
③由题意![]() ,根据△ABC上所有点到y轴的距离都不小于1,构建不等式即可解决问题.
,根据△ABC上所有点到y轴的距离都不小于1,构建不等式即可解决问题.
(2)由题意AB=![]() ,由△ABD是以AB为斜边的等腰直角三角形,推出点D到AB的距离为1,分两种情形分别求解即可解决问题.
,由△ABD是以AB为斜边的等腰直角三角形,推出点D到AB的距离为1,分两种情形分别求解即可解决问题.
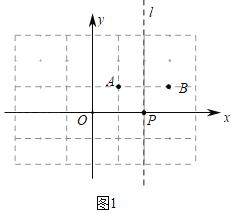
解:(1)①如图1中,
当![]()
![]()
![]() A(1,1),A,B关于直线x=2对称,
A(1,1),A,B关于直线x=2对称,
∴B(3,1).
故答案为(3,1).
②如图2中,当![]()
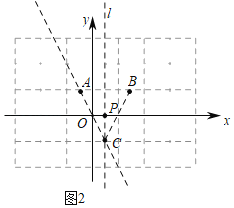
![]() A(﹣0.5,1),
A(﹣0.5,1),![]() ,直线l:x=0.5,
,直线l:x=0.5,
设![]() 为
为![]() ,
,
![]()
![]()
![]() 在
在![]() 上,
上,
![]() 直线AC的解析式为y=﹣2x,
直线AC的解析式为y=﹣2x,
∴C(0.5,﹣1),
∴点C到x轴的距离为1,
故答案为1.
③由题意![]() ,
,
∵![]() 上所有点到y轴的距离都不小于1,
上所有点到y轴的距离都不小于1,
∴t﹣1≥1或t+1≤﹣1,
解得![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.
(2)如图3中,
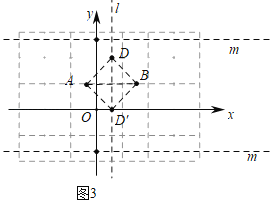
∵![]() ,
,
∴AB=![]()
∵![]() 是以AB为斜边的等腰直角三角形,
是以AB为斜边的等腰直角三角形,
∴点D到AB的距离为1,
∴当点D在AB上方时,若直线m上存在点P,![]() 上存在点K,满足PK=1,则
上存在点K,满足PK=1,则![]() .
.
当点D在AB下方时,若直线m上存在点P,![]() 上存在点K,满足PK=1,则
上存在点K,满足PK=1,则![]() .
.
综上:![]() 的取值范围是:
的取值范围是:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,△ADC与△ABC关于直线AC对称,AE与CD垂直交BC的延长线于点E,∠EAF=45°,且AF与AB在AE的两侧,EF⊥AF.
(1)依题意补全图形.
(2)①在AE上找一点P,使点P到点B,点C的距离和最短;
②求证:点D到AF,EF的距离相等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小苏和小林在如图所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如下图所示.下列叙述正确的是( )

A. 两人从起跑线同时出发,同时到达终点.
B. 小苏跑全程的平均速度大于小林跑全程的平均速度.
C. 小苏在跑最后100m的过程中,与小林相遇2次.
D. 小苏前15s跑过的路程小于小林前15s跑过的路程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求若干个相同的不为零的有理数的除法运算叫做除方.
如:2÷2÷2,(-3)÷(-3)÷(-3 )÷( -3)等. 类比有理数的乘方,我们把 2÷2÷2 记作 2③,读作“2 的圈 3 次方”. (-3)÷(-3)÷(-3 )÷( -3)记作(-3)④,读作“-3 的圈 4 次方”.
一般地,把
 (a≠0)记作
(a≠0)记作 ,读作“a的圈n次方”.
,读作“a的圈n次方”.(1)直接写出计算结果:
 _____,
_____,  _________,
_________,  ___________,
___________,(2)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,
请尝试将有理数的除方运算转化为乘方运算,归纳如下:一个非零有理数的圈 n 次方等于_____.
(3)计算
 .
. -
科目: 来源: 题型:
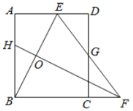
查看答案和解析>>【题目】如图,矩形ABCD中,AB=12,点E是AD上的一点,AE=6,BE的垂直平分线交BC的延长线于点F,连接EF交CD于点G.若G是CD的中点,则BC的长是__________.
-
科目: 来源: 题型:
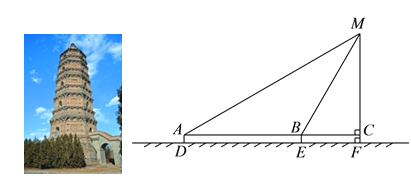
查看答案和解析>>【题目】某校九年级数学兴趣小组的同学进行社会实践活动时,想利用所学的解直角三角形的知识测量某塔的高度,他们先在点
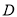 用高
用高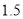 米的测角仪
米的测角仪 测得塔顶
测得塔顶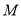 的仰角为
的仰角为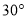 ,然后沿
,然后沿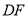 方向前行
方向前行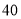 m到达点
m到达点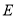 处,在
处,在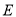 处测得塔顶
处测得塔顶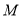 的仰角为
的仰角为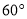 .请根据他们的测量数据求此塔
.请根据他们的测量数据求此塔 的高.(结果精确到
的高.(结果精确到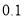 m,参考数据:
m,参考数据: 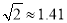 ,
, 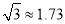 ,
,  )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面
的最大距离是5m.
(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如下图)
你选择的方案是_____(填方案一,方案二,或方案三),则B点坐标是______,求出你所选方案中的抛物线的表达式;
(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.


相关试题

