【题目】(7分)如图,已知抛物线y=x2+bx+c经过A(-1,0),B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,求y的取值范围;
(3)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标.

参考答案:
【答案】(1)y=(x﹣1)2﹣4,(1,﹣4).(2) 0<x<3;(3)P点坐标为(﹣2,5)或(4,5).
【解析】(1)把A(﹣1,0)、B(3,0)分别代入y=x2+bx+c中,
得: ![]() ,解得:
,解得: ![]() ,
,
∴抛物线的解析式为y=x2﹣2x﹣3.
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,∴顶点坐标为(1,﹣4).
(2)由图可得当0<x<3时,﹣4≤y<0.
(3)∵A(﹣1,0)、B(3,0),∴AB=4.
设P(x,y),则S△PAB=![]() AB|y|=2|y|=10,∴|y|=5,∴y=±5.
AB|y|=2|y|=10,∴|y|=5,∴y=±5.
①当y=5时,x2﹣2x﹣3=5,解得:x1=﹣2,x2=4,
此时P点坐标为(﹣2,5)或(4,5);
②当y=﹣5时,x2﹣2x﹣3=﹣5,方程无解;
综上所述,P点坐标为(﹣2,5)或(4,5).
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出命题:“直角都相等”的逆命题:_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了从甲、乙两名选手中选拔出一名参加射击比赛,现对他们的射击水平进行一次测验,两个人在相同条件下各射靶10次,为了比较两个人的成绩,制作了如下统计图表:
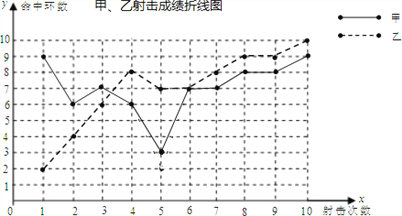
甲、乙射击成绩统计表

(1)请补全上述统计表.
(2)如果规定成绩较稳定者胜出,你认为谁胜出?请说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:f(a,b)=(b,a),g(m,n)=(﹣m,﹣n).例如f(2,3)=(3,2),g(﹣1,﹣4)=(1,4).则g[f(﹣5,6)]等于( )
A.(﹣6,5)B.(﹣5,﹣6)C.(6,﹣5)D.(﹣5,6)
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读新知:移项且合并同类项之后,只含有偶次项的四次方程称作双二次方程.其一般形式为ax4+bx2+c=0(a≠0),一般通过换元法解之,具体解法是设 x2=y,则原四次方程化为一元二次方程:ay2+by+c=0,解出y之后代入x2=y,从而求出x的值.
例如解:4x4-8x2+3=0
解:设x2=y,则原方程可化为:4y2-8y+3=0
∵a=4,b=-8,c=3
∴b2-4ac=(-8)2-4×4×3=16>0
∴y=
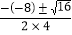 =
=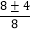
∴y1=
 , y2=
, y2=
∴当y1=
 时,x2=
时,x2= . ∴x1=
. ∴x1= ,x2=-
,x2=- ;
;当y1=
 时,x2=
时,x2= . ∴x3=
. ∴x3= ,x4=-
,x4=- .
.小试牛刀:请你解双二次方程:x4-2x2-8=0
归纳提高:
思考以上解题方法,试判断双二次方程的根的情况,下列说法正确的是____________(选出所有的正确答案)
①当b2-4ac≥0时,原方程一定有实数根;
②当b2-4ac<0时,原方程一定没有实数根;
③当b2-4ac≥0,并且换元之后的一元二次方程有两个正实数根时,原方程有4个实数根,换元之后的一元二次方程有一个正实数根一个负实数根时,原方程有2个实数根;
④原方程无实数根时,一定有b2-4ac<0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2x+1>3的解集是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次数学测试中,某学习小组5人的成绩分别是120、100、135、100、125,则他们成绩的中位数是.
相关试题

