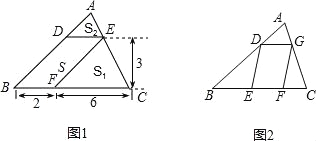
【题目】问题背景(1)如图1,△ABC中,DE∥BC分别交AB,AC于D,E两点,过点E作EF∥AB交BC于点F.请按图示数据填空:△EFC的面积S1= ,△ADE的面积S2= .
探究发现(2)在(1)中,若BF=m,FC=n,DE与BC间的距离为h.请证明S2=4S1S2.
拓展迁移(3)如图2,DEFG的四个顶点在△ABC的三边上,若△ADG、△DBE、△GFC的面积分别为3、7、5,试利用(2)中的结论求△ABC的面积.
参考答案:
【答案】(1)9;1;(2)证明见解析;(3)27.
【解析】
试题分析:(1)△EFC的面积利用底×高的一半计算;△ADE的面积,可以先过点A作AH⊥BC,交DE于G,交BC于H,即AG是△ADE的高,AH是△ABC的高,利用平行线分线段成比例定理的推论,可知△ADE∽△ABC,利用相似三角形的性质可求AG,再利用三角形的面积公式计算即可;
(2)由于DE∥BC,EF∥AB,可知四边形DBFE是平行四边形,同时,利用平行线分线段成比例定理的推论,可知△ADE∽△ABC,△EFC∽△ABC,从而易得△ADE∽△EFC,利用相似三角形的面积比等于相似比的平方,可得S1:S2=n2:m2,由于S1=![]() nh,那么可求S2,从而易求4S1S2,又S=mh,容易证出结论;
nh,那么可求S2,从而易求4S1S2,又S=mh,容易证出结论;
(3)过点G作GH∥AB交BC于H,则四边形DBHG为平行四边形,容易证出△DBE≌△GHF,那么△GHC的面积等于8,再利用(2)中的结论,可求DBHG的面积,从而可求△ABC的面积.
试题解析:(1)S1=![]() ×6×3=9,
×6×3=9,
过A作AH⊥BC,交DE于G,
∵DE∥BC,EF∥AB,
∴四边形DEFB是平行四边形,
∴DE=BF=2,
∵DE∥BC,
∴AG⊥DE,△ADE∽△ABC,
∴![]() ,
,
∴![]() ,
,
解得:AG=1,
∴S2=![]() ×DE×AG=
×DE×AG=![]() =1,
=1,
(2)∵DE∥BC,EF∥AB,
∴四边形DBFE为平行四边形,∠AED=∠C,∠A=∠CEF,
∴△ADE∽△EFC,
∴![]() ,
,
∵S1=![]() nh,
nh,
∴S2=![]() ×S1=
×S1=![]() ,
,
∴4S1S2=4×![]() nh×
nh×![]() =(mh)2,
=(mh)2,
而S=mh,
∴S2=4S1S2;
(3)过点G作GH∥AB交BC于H,则四边形DBHG为平行四边形,
∴∠GHC=∠B,BD=HG,DG=BH,
∵四边形DEFG为平行四边形,∴DG=EF,
∴BH=EF,
∴BE=HF,
在△DBE和△GHF中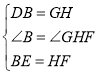 ,
,
∴△DBE≌△GHF(SAS),
∴△GHC的面积为7+5=12,
由(2)得,平行四边形DBHG的面积S为![]() =12,
=12,
∴△ABC的面积为3+12+12=27.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程(2+x)(3x﹣4)=5的二次项系数是_____,一次项系数是_____,常数项是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 全等的两个图形成中心对称
B. 成中心对称的两个图形必须能完全重合
C. 旋转后能重合的两个图形成中心对称
D. 成中心对称的两个图形不一定全等
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列方程化为一元二次方程的一般形式.
(1)(1﹣2x)(x﹣1)=0;
(2)2(x﹣l)+6x﹣7=2x2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
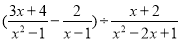 ,其中x是不等式组
,其中x是不等式组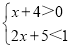 的整数解.
的整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】当k取何值时,关于x的方程(k2﹣1)x2+(k﹣1)x+1=0是一元二次方程?
相关试题

