【题目】如图,已知AD是△ABC的角平分线,CE是△ABC的高,AD与CE相交于点P,∠BAC=66°,∠BCE=40°,求∠ADC和∠APC的度数.
参考答案:
【答案】解:∵AD是△ABC的角平分线,∠BAC=66°,
∴∠DAC=∠BAD=33°,
∵CE是△ABC的高,∠BCE=40°,
∴∠B=50°,
∠ACB=180°-50°-66°=64°;
∴∠ADC=180°-64°-33°=83°,∠APC=123°
【解析】在直角三角形BCE中∠BCE=40°,可求出∠B=50°,由三角形内角和可求出∠BCA的度数;由AD是∠BAC的角平分线易求∠ADC的度数,再由CE⊥AB易求∠ACE的度数,从而可求∠APC的度数.
【考点精析】认真审题,首先需要了解三角形的“三线”(1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内),还要掌握三角形的内角和外角(三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区2016年屋顶绿化面积为2000平方米,计划2018年屋顶绿化面积要达到2880平方米,如果每年屋顶绿化面积的增长率相同,那么这个增长率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:3x3﹣[x3﹣3y+(6x2﹣7x)]﹣2(x3﹣3x2﹣4x+y),其中x=﹣1,y=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB内一点P,P1 , P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若△PMN的周长是5cm,则P1P2的长为( )
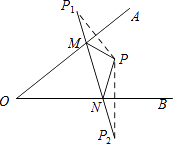
A.3cm
B.4cm
C.5cm
D.6cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:四边形ABCD为平行四边形,延长AD至E,使DE=AD,连接EB,EC,DB.添加一个条件,不能使四边形DBCE为矩形的是( )

A. AB=BE B. BE⊥CD C. ∠ADB=900 D. CE⊥DE
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠A=30°,∠B=62°,CE平分∠ACB,CD⊥AB于D,DF⊥CE于F,求∠CDF的度数.
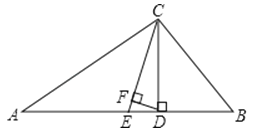
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某天的最高气温是8℃,最低气温是-1℃,那么当天的最大温差是
相关试题

