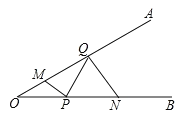
【题目】如图,∠AOB=30°,M、N分别在OA、OB上,且OM=2,ON=4,点P、Q分别在OB、OA上,则MP+PQ+QN的最小值是 _______.
参考答案:
【答案】2![]()
【解析】
作M关于OB的对称点M',作N关于OA的对称点N',连接M'N',可以得出M'N'即为MP+PQ+QN的最小值;证出△ONN'为等边三角形,△OMM'为等边三角形,得出∠N'OM'=90°,由勾股定理求出M'N'即可.
作M关于OB的对称点M',作N关于OA的对称点N',如图所示:
连接M'N'交OB于点P,交OA于点Q,连接MP,PQ,QN,则MP+PQ+QN=M'P+PQ+QN'=M'N',∴M'N'为MP+PQ+QN的最小值.
根据轴对称的定义可知:∠N'OQ=∠M'OB=30°,∠ONN'=60°,∴△ONN'为等边三角形,△OMM'为等边三角形,∴∠N'OM'=90°ON'=ON=4,OM'=OM=2,∴在Rt△M'ON'中,M'N'![]() .
.
故答案为:2![]() .
.

-
科目: 来源: 题型:
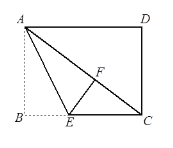
查看答案和解析>>【题目】如图,已知在长方形ABCD中,将△ABE沿着AE折叠至△AEF的位置,点F在对角线AC上,若BE=3,EC=5,则线段CD的长是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织学生到外地进行社会实践活动,共有680名学生参加,并携带300件行李.学校计划租用甲、乙两种型号的汽车共20辆.经了解,甲种汽车每辆最多能载40人和10件行李,乙种汽车每辆最多能载30人和20件行李.
(1)如何安排甲、乙两种汽车可一次性地将学生和行李全部运走?有哪几种方案?
(2)如果甲、乙两种汽车每辆的租车费用分别为2000元、1800元,请你选择最省钱的一种租车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1) 已知3×9m×27m=321,求m的值.
(2)(
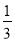 )﹣2+(2019﹣π)0÷(﹣2)﹣2﹣32;
)﹣2+(2019﹣π)0÷(﹣2)﹣2﹣32;(3)已知:
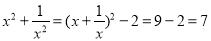 ,求 ①
,求 ①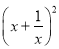 ,②
,② ,③
,③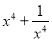 的值
的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)对于算式2(3+1)(32+1)(34+1)(38+1)+1
不用计算器,你能计算出来吗?
(2)你知道它的计算结果的个位是几吗?
(3)根据(1)推测(a+1)(a2+1)(a4+1)(a8+1)(a16+1)…(a1024+1)= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x
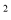 -ax+a
-ax+a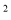 -4a-4与x轴相交于点A和点B,与y轴相交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C,动点P以每秒2个单位长度的速度从C点出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从点A出发,沿A→B运动,连接PQ、CB,设点P运动的时间为t秒.
-4a-4与x轴相交于点A和点B,与y轴相交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C,动点P以每秒2个单位长度的速度从C点出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从点A出发,沿A→B运动,连接PQ、CB,设点P运动的时间为t秒.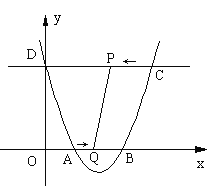
(1)求a的值;(2)当四边形ODPQ为矩形时,求这个矩形的面积;(3)当四边形PQBC的面积等于14时,求t的值.(4)当t为何值时,△PBQ是等腰三角形?(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC∶∠AOD=7∶11.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.

相关试题

