搜索
【题目】如图，△ABC中，AB=AC ， AD平分∠BAC ， DE∥AC交AB于E ， 则S△EBD：S△ABC=（ ） 
A.1：2
B.1：4
C.1：3
D.2：3
参考答案：
【答案】B
【解析】解答：如图，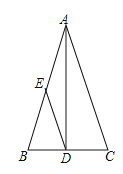
∵在△ABC中，AB=AC ， AD平分∠BAC ，
∴点D是BC的中点 ．
又∵DE∥AC ，
∴ED是△ABC的中位线，且△EBD∽△ABC ，
∴相似比是：ED：AC=1：2，
∴S△EBD：S△ABC=1：4 ．
故选：B.
分析：易证ED是△ABC的中位线，相似三角形△EBD∽△ABC的相似比是1：2；然后由相似三角形的面积之比等于相似比的平方进行答题 ．
【考点精析】利用三角形中位线定理对题目进行判断即可得到答案，需要熟知连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，D，E分别是边BC，AC上的点，且BD=EC，∠ADE=∠B.
(1)求证：AD=DE；
(2)若∠ADE=
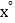,求∠ADB的度数(用含x的代数式表示).
-
科目： 来源： 题型：
查看答案和解析>>【题目】连接四边形不相邻两个顶点的线段叫做四边形的对角线，如图1，四边形ABCD中线段AC、线段BD就是四边形ABCD 的对角线.把对角线互相垂直的四边形叫做垂美四边形．
（1）概念理解：如图2，在四边形ABCD中，AB=AD，CB=CD，问四边形ABCD是垂美四边形吗？请说明理由．
（2）性质探究：试探索垂美四边形ABCD两组对边AB，CD的平方和与BC，AD的平方和之间的数量关系．
猜想结论：（要求用文字语言叙述）______
写出证明过程（先画出图形，写出已知、求证）．
（3）问题解决：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG，GE，已知AC=4，AB=5，求GE长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，点D、E分别是边AB，BC的中点．若△DBE的周长是6，则△ABC的周长是（ ）
A.8
B.10
C.12
D.14 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，∠A=90°，BC∥AD，AB=6cm，点P从A出发沿射线AD运动，速度是每秒1cm，点R从点B出发沿射线BC运动，速度是每秒2cm，点Q在点P的右侧，且PQ=10cm，时间为t秒；
求：（1）△PQR的面积；
（2）当t=1秒时，求PR的长；
（3）当t为何值时，△PQR是等腰三角形？
-
科目： 来源： 题型：
查看答案和解析>>【题目】顺次连接四边形各边中点所得的四边形是（ ）
A.平行四边形
B.矩形
C.菱形
D.以上都不对 -
科目： 来源： 题型：
查看答案和解析>>【题目】三种不同类型的纸板的长宽如图所示，其中A类和C类是正方形，B类是长方形，现A类有1块，B类有4块，C类有5块. 如果用这些纸板拼成一个正方形，发现多出其中1块纸板，那么拼成的正方形的边长是（ ）
A. m+n B. 2m+2n C. 2m+n D. m+2n
相关试题
