【题目】某巡警骑摩托车在一条南北大道上巡逻,某天他从岗亭出发,晚上停留在A处,规定向北方向为正,当天行驶情况记录如下(单位:千米):
+10,﹣8,+7,﹣15,+6,﹣16,+4,﹣2
(1)A处在岗亭何方?距离岗亭多远?
(2)若摩托车每行驶1千米耗油a升,这一天共耗油多少升?
参考答案:
【答案】(1)A处在岗亭南方,距离岗亭14千米;(2)这一天共耗油68a升.
【解析】解:(1)10-8+7-15+6-16+4-2=-14……………………………………(3分)
B处在A处正南方14千米处。 (1分)
(2)|10|+|-8|+|7|+|-15|+|6|+|-16|+|4|+|-2|=68(千米)……..(2分)
68×a=68a(升)
答:共耗油68a升。
(1)根据所有数据的和即可解答
(2)把所有数据的绝对值相加,求得总路程,根据每行驶1千米耗油![]() 升,即可求得一天共耗油多少升
升,即可求得一天共耗油多少升
-
科目: 来源: 题型:
查看答案和解析>>【题目】青山村种的水稻2010年平均每公顷产7200kg,2012年水稻平均每公顷产的产量是8400kg,设水稻每公顷产量的年平均增长率为x,可列方程为( )
A.7200(1+x)2=8400B.7200(1+x2)=8400
C.7200(x2+x)=8400D.7200(1+x)=8400
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
1
°
x
7
﹣3
…
(1)可知x= ,= ,°= ;
(2)试判断第2016个格子中的数是多少?并给出相应的理由.
(3)判断:前n个格子中所填整数之和是否可能为2016?若能,求出n的值,若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列多项式中,能分解因式的是( )
A. a2+b2 B. ﹣a2﹣b2 C. a2﹣4a+4 D. a2+ab+b2
-
科目: 来源: 题型:
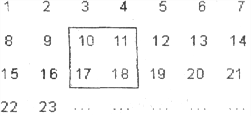
查看答案和解析>>【题目】把正整数1,2,3,4,……,2009排列成如图所示的一个表
(1)用一正方形在表中随意框住4个数,把其中最小的数记为x,另三个数用含x的式子表示出来,从小到大依次是 , , 。
(2)当被框住的4个数之和等于416时,x的值是多少?
(3)被框住的4个数之和能否等于622?如果能,请求出此时x的值;如果不能,请说明理由。
-
科目: 来源: 题型:
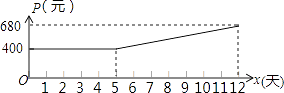
查看答案和解析>>【题目】某市制药厂需要紧急生产一批药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量y(吨)是时间x(天)一次函数,且满足表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本P(元)与时间x(天)的关系满足图中的函数图象.
时间x(天)
2
4
每天产量y(吨)
24
28
(1)求药品每天的产量y(吨)是时间x(天)之间的函数关系式;
(2)当5≤x≤12时,直接写出P(元)与时间x(天)的函数关系是P=;
(3)若这批药品的价格为1400元/吨,每天的利润设为W元,求哪一天的利润最高,最高利润是多少?(利润=价格﹣成本)
(4)为了提高工人加班的津贴,药厂决定在(3)中价格的基础上每吨药品加价a元,但必须满足从第5天到第12天期间,每吨加价a后每天的利润随时间的增大而增大,直线写出a的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一些相同的房间需要粉刷墙面,一天4名一级技工去粉刷10个房间,结果其中有
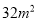 墙面未来得及粉刷;同样时间内7名二级技工粉刷了15个房间之外,还多粉刷了另外的
墙面未来得及粉刷;同样时间内7名二级技工粉刷了15个房间之外,还多粉刷了另外的 墙面.每名一级技工比二级技工一天多粉刷
墙面.每名一级技工比二级技工一天多粉刷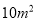 墙面.设每个房间需要粉刷的墙面面积为
墙面.设每个房间需要粉刷的墙面面积为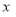 平方米,一级技工每天粉刷y平方米,下列方程正确有( )个
平方米,一级技工每天粉刷y平方米,下列方程正确有( )个(1)
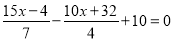 (2)
(2)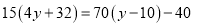
(3)
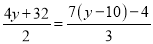 (4)
(4)
A. 4 B. 3 C. 2 D. 1
相关试题

