Question

【题目】如图，已知抛物线经过原点O，顶点为A（1，1），且与直线y=x﹣2交于B，C两点．

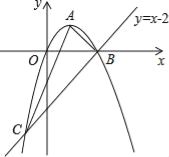
（1）求抛物线的解析式及点C的坐标；

（2）求证：△ABC是直角三角形；

（3）若点N为x轴上的一个动点，过点N作MN⊥x轴与抛物线交于点M，则是否存在以O，M，N为顶点的三角形与△ABC相似？若存在，请求出点N的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）y=﹣x2+2x；C（-1，-3）；（2）证明过程见解析；（3）（，0）或（，0）或（﹣1，0）或（5，0）

【解析】

试题分析：（1）可设顶点式，把原点坐标代入可求得抛物线解析式，联立直线与抛物线解析式，可求得C点坐标；（2）分别过A、C两点作x轴的垂线，交x轴于点D、E两点，结合A、B、C三点的坐标可求得∠ABO=∠CBO=45°，可证得结论；（3）设出N点坐标，可表示出M点坐标，从而可表示出MN、ON的长度，当△MON和△ABC相似时，利用三角形相似的性质可得=或=，可求得N点的坐标．

试题解析：（1）∵顶点坐标为（1，1）， ∴设抛物线解析式为y=a（x﹣1）2+1，

又抛物线过原点， ∴0=a（0﹣1）2+1，解得a=﹣1， ∴抛物线解析式为y=﹣（x﹣1）2+1， 即y=﹣x2+2x，

联立抛物线和直线解析式可得，解得或，

∴B（2，0），C（﹣1，﹣3）；

（2）如图，分别过A、C两点作x轴的垂线，交x轴于点D、E两点，

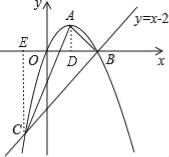
则AD=OD=BD=1，BE=OB+OE=2+1=3，EC=3， ∴∠ABO=∠CBO=45°，即∠ABC=90°， ∴△ABC是直角三角形；

（3）假设存在满足条件的点N，设N（x，0），则M（x，﹣x2+2x），

∴ON=|x|，MN=|﹣x2+2x|， 由（2）在Rt△ABD和Rt△CEB中，可分别求得AB=，BC=3，

∵MN⊥x轴于点N ∴∠ABC=∠MNO=90°， ∴当△ABC和△MNO相似时有=或=，

①当=时，则有=，即|x||﹣x+2|=|x|，

∵当x=0时M、O、N不能构成三角形， ∴x≠0， ∴|﹣x+2|=，即﹣x+2=±，解得x=或x=，

此时N点坐标为（，0）或（，0）；

②当=时，则有=，即|x||﹣x+2|=3|x|，

∴|﹣x+2|=3，即﹣x+2=±3，解得x=5或x=﹣1， 此时N点坐标为（﹣1，0）或（5，0），

综上可知存在满足条件的N点，其坐标为（，0）或（，0）或（﹣1，0）或（5，0）．