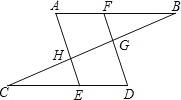
【题目】已知,如图,点F在AB上,点E在CD上,AE、DF分别交BC与H,G,∠A=∠D,∠FGB+∠EHG=180°.
(1)求证:AB∥CD;
(2)若AE⊥BC,直接写出图中所有与∠C互余的角,不需要证明.
参考答案:
【答案】(1)详见解析;(2)与∠C互余的角有∠AEC、∠A、∠D、∠BFG.
【解析】
(1)由∠FGB+∠EHG=180°易得AE∥DF,从而有∠A+∠AFD=180°,又因∠A=∠D,所以∠D+∠AFD=180°,则AB∥CD. (2)利用平行线性质,进行角度替换可得到与∠C互余的角有∠AEC、∠A、∠D、∠BFG.
解:(1)∵∠FGB+∠EHG=180°,
∴∠HGD+∠EHG=180°,
∴AE∥DF,
∴∠A+∠AFD=180°,
又∵∠A=∠D,
∴∠D+∠AFD=180°,
∴AB∥CD.
(2)∵AE⊥BC,
∴∠CHE=90°,
∴∠C+∠AEC=90°,即∠C与∠AEC互余,
∵AE∥DF,
∴∠AEC=∠D,∠A=∠BFG,
∵AB∥CD,
∴∠AEC=∠A,
综上,与∠C互余的角有∠AEC、∠A、∠D、∠BFG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】养成良好的早锻炼习惯,对学生的学习和生活都非常有益,某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间x(分钟)进行了调查.现把调查结果分成A、B、C、D四组,如表所示,同时,将调查结果绘制成下面两幅不完整的统计图.
分组
A
B
C
D
x(分钟)的范围
0≤x<10
10≤x<20
20≤x<30
30≤x<40
请你根据以上提供的信息,解答下列问题:

(1)补全频数分布直方图;
(2)所抽取的七年级学生早锻炼时间的中位数落在______组内(填“A”或“B”或“C”或“D”);
(3)已知该校七年级共有1200名学生,请你估计这个年级学生中约有多少人一天早锻炼的时间不少于20分钟.(早锻炼:指学生在早晨7:00~7:40之间的锻炼)
-
科目: 来源: 题型:
查看答案和解析>>【题目】光明电器超市销售每台进价分别为190元、160元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
2台
6台
1840元
第二周
5台
7台
2840 元
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备再采购这两种型号的电风扇共40台,这40台电风扇全部售出后,若利润不低于2660元,求A种型号的电风扇至少要采购多少台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
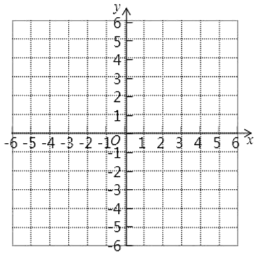
(1)先作出△ABC,再将△ABC向下平移5个单位长度后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得得到△A2B2C2,请画出△A2B2C2;
(3)求出以O,A1,B为顶点的三角形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.

(1)求证:四边形DEFG是平行四边形;
(2)如果∠OBC=45°,∠OCB=30°,OC=4,求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】商场某柜台销售每台进价分别为160元、120元的A.B两种型号的电风扇,下表是近两周的销售情况:
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
4台
1200元
第二周
5台
6台
1900元
(进价、售价均保持不变,利润=销售收入进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,请问商场销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点P是等边△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.
(1)求证:PB=QC;
(2)若∠APB=150°,PA=9,PB=12,求PC的长度.

相关试题

