【题目】某服装厂生产一种西装和领带,西装每套定价![]() 元,领带每条定价
元,领带每条定价![]() 元,厂方在开展促销活动期间,向客户提供两种优惠方案:
元,厂方在开展促销活动期间,向客户提供两种优惠方案:
①西装和领带都按定价的![]() 付款;②买一套西装送一条领带。
付款;②买一套西装送一条领带。
现某客户要到该服装厂购买西装![]() 套,领带
套,领带![]() 条
条![]() 。
。
(1)若该客户按方案①购买,需付款多少元?(用含![]() 的代数式表示);
的代数式表示);
(2)若该客户按方案②购买,需付款多少元?(用含![]() 的代数式表示);
的代数式表示);
(3)若![]() ,通过计算说明此时按哪种方案购买较为合算?
,通过计算说明此时按哪种方案购买较为合算?
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)方案②比较合算.
;(3)方案②比较合算.
【解析】
(1)根据西装和领带都按定价的![]() 付款列代数式即可;
付款列代数式即可;
(2)根据买一套西装送一条领带列代数式即可;
(3)把x=30代入(1)(2)中的代数式中计算对应的值,然后比较它们的大小可判断按哪种方案购买较为合算.
解:(1)按方案①购买,付款为:400×0.9×20+0.9×100x=90x+7200;
(2)按方案②购买,付款为:400×20+(x20)×100=100x+6000;
(3)当x=30时,
方案①:90x+7200=90×30+7200=9900(元),
方案②:100x+6000=100×30+6000=9000(元),
∵9000<9900,
∴按方案②购买较为合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点
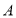 、点
、点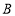 表示的数分别为
表示的数分别为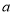 、
、 ,则
,则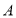 、
、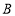 两点之间的距离
两点之间的距离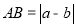 ,线段
,线段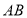 的中点表示的数为
的中点表示的数为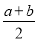 .
.(问题情境)
如图,数轴上点
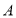 表示的数为
表示的数为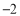 ,点
,点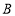 表示的数为8,点
表示的数为8,点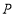 从点
从点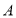 出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点
出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点 从点
从点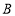 出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为
出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为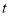 秒(
秒( ).
).(综合运用)
(1)填空:
①
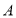 、
、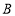 两点之间的距离
两点之间的距离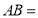 ________,线段
________,线段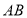 的中点表示的数为__________.
的中点表示的数为__________.②用含
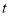 的代数式表示:
的代数式表示: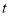 秒后,点
秒后,点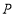 表示的数为____________;点
表示的数为____________;点 表示的数为___________.
表示的数为___________.③当
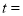 _________时,
_________时,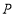 、
、 两点相遇,相遇点所表示的数为__________.
两点相遇,相遇点所表示的数为__________.(2)当
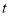 为何值时,
为何值时,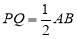 .
.(3)若点
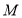 为
为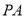 的中点,点
的中点,点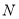 为
为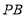 的中点,点
的中点,点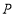 在运动过程中,线段
在运动过程中,线段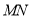 的长度是否发生变化?若变化,请说明理由;若不变,请求出线段
的长度是否发生变化?若变化,请说明理由;若不变,请求出线段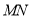 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小兵两人参加体育项目训练,近期的5次测试成绩如下表所示:
1次
2次
3次
4次
5次
小明
10
14
13
12
13
小兵
11
11
15
14
11
根据以上信息,解决以下问题:
(1)小明成绩的中位数是__________.
(2)小兵成绩的平均数是__________.
(3)为了比较他俩谁的成绩更稳定,老师利用方差公式计算出小明的方差如下(其中
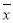 表示小明的平均成绩);
表示小明的平均成绩); 
请你帮老师求出小兵的方差,并比较谁的成绩更稳定。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为
 ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
【答案】(1)证明见解析;(2)

【解析】试题分析:(1)首先连接OD,由OE∥AB,根据平行线与等腰三角形的性质,易证得
 ≌
≌ 即可得
即可得 ,则可证得
,则可证得 为
为 的切线;
的切线;
(2)连接CD,根据直径所对的圆周角是直角,即可得 利用勾股定理即可求得
利用勾股定理即可求得 的长,又由OE∥AB,证得
的长,又由OE∥AB,证得 根据相似三角形的对应边成比例,即可求得
根据相似三角形的对应边成比例,即可求得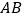 的长,然后利用三角函数的知识,求得
的长,然后利用三角函数的知识,求得 与
与 的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.试题解析:(1)证明:连接OD,

∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
∴ED⊥OD,
∴ED是
 的切线;
的切线;(2)连接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,

∵OE∥AB,
∴△COE∽△CAB,
 ∴AB=5,
∴AB=5,∵AC是直径,




∵EF∥AB,



∴S△ADF=S梯形ABEFS梯形DBEF

∴△ADF的面积为


【题型】解答题
【结束】
25【题目】【题目】已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.

-
科目: 来源: 题型:
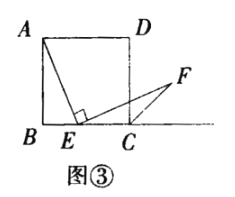
查看答案和解析>>【题目】如图①,四边形
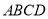 是正方形,点
是正方形,点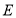 是边
是边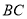 的中点,
的中点,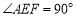 ,且
,且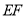 交正方形的外角平分线
交正方形的外角平分线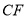 于点
于点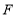 请你认真阅读下面关于这个图形的探究片段,完成所提出的问题.
请你认真阅读下面关于这个图形的探究片段,完成所提出的问题.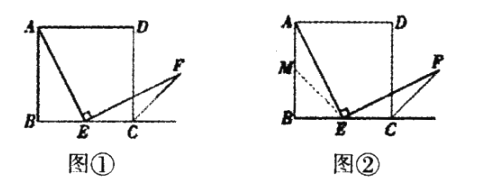
(1)探究1:小强看到图①后,很快发现
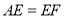 这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(个直角三角形,一个钝角三角形)考虑到点E是边BC的中点,因此可以选取AB的中点M(如图②),连接EM后尝试着去证明
这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(个直角三角形,一个钝角三角形)考虑到点E是边BC的中点,因此可以选取AB的中点M(如图②),连接EM后尝试着去证明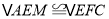 就行了.随即小强写出了如下的证明过程:
就行了.随即小强写出了如下的证明过程:证明:如图②,取AB的中点M,连接EM.
∵
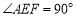
∴

又∵
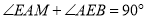
∴
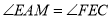
∵点E、M分别为正方形的边BC和AB的中点,
∴
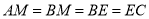
∴
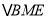 是等腰直角三角形,
是等腰直角三角形,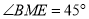
∴
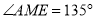
又∵
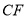 是正方形外角的平分线,
是正方形外角的平分线,∴
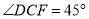 ,∴
,∴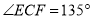
∴
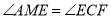
∴
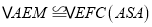 ,
,∴
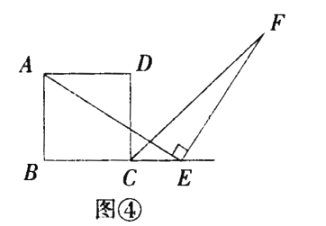
(2)探究2:小强继续探索,如图③,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,发现AE=EF仍然成立小强进一步还想试试,如图④,若把条件“点E是边BC的中点”为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF仍然成立请你选择图③或图④中的一种情况写出证明过程给小强看.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a,b,c在数轴上的位置如图所示,且表示数a的点、数b的点与原点的距离相等.
(1)用“>”“<”或“=”填空:b______0,a+b______0,a-c______0,b-c______0;
(2)|b-1|+|a-1|=________;
(3)化简:|a+b|+|a-c|-|b|+|b-c|.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车分别从
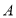 、
、 两地同时出发,甲车匀速前往
两地同时出发,甲车匀速前往 地,到达
地,到达 地后立即以另一速度按原路匀速返回到
地后立即以另一速度按原路匀速返回到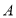 地; 乙车匀速前往
地; 乙车匀速前往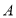 地,设甲、乙两车距
地,设甲、乙两车距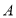 地的路程为
地的路程为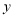 (千米),甲车行驶的时间为
(千米),甲车行驶的时间为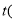 时),
时), 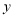 与
与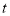 之间的函数图象如图所示
之间的函数图象如图所示(1)甲车从
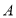 地到
地到 地的速度是__________千米/时,乙车的速度是__________千米/时;
地的速度是__________千米/时,乙车的速度是__________千米/时; (2)求甲车从
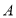 地到达
地到达 地的行驶时间;
地的行驶时间; (3)求甲车返回时
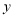 与
与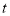 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量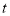 的取值范围;
的取值范围; (4)求乙车到达
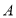 地时甲车距
地时甲车距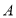 地的路程.
地的路程.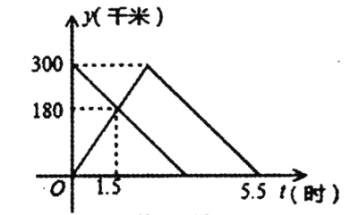
相关试题

