【题目】如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF= ![]() CD,求证:∠AEF=90°.
CD,求证:∠AEF=90°. 
参考答案:
【答案】证明:∵ABCD为正方形,
∴AB=BC=CD=DA,∠B=∠C=∠D=90°.
设AB=BC=CD=DA=a,
∵E是BC的中点,且CF= ![]() CD,
CD,
∴BE=EC= ![]() a,CF=
a,CF= ![]() a,
a,
在Rt△ABE中,由勾股定理可得AE2=AB2+BE2= ![]() a2,
a2,
同理可得:EF2=EC2+FC2= ![]() a2,AF2=AD2+DF2=
a2,AF2=AD2+DF2= ![]() a2,
a2,
∵AE2+EF2=AF2,
∴△AEF为直角三角形,
∴∠AEF=90°.
【解析】利用正方形的性质得出AB=BC=CD=DA,∠B=∠C=∠D=90°,设出边长为a,进一步利用勾股定理求得AE、EF、AF的长,再利用勾股定理逆定理判定即可.
【考点精析】本题主要考查了勾股定理的概念和勾股定理的逆定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】650万用科学记数法表示应是( )
A.0.65×107
B.6.5×106
C.65×105
D.65×106 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
 (a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1和3,则下列结论正确的是( )
(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1和3,则下列结论正确的是( )
A. 2a﹣b=0
B. a+b+c>0
C. 3a﹣c=0
D. 当a=
 时,△ABD是等腰直角三角形
时,△ABD是等腰直角三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
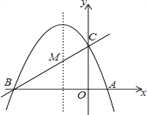
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点M(2﹣a,3a+6)到两坐标轴的距离相等,则M点坐标_________
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知图1将线段AB向右平移1个单位长度,图2是将线段AB折一下再向右平移1个单位长度,请在图3中画出一条有两个折点的折线向右平移1个单位长度的图形;

(2)若长方形的长为a,宽为b,请分别写出三个图形中除去阴影部分后剩下部分的面积;
(3)如图4,在宽为10 m,长为40 m的长方形菜地上有一条弯曲的小路,小路宽度为1 m,求这块菜地的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1:y=kx+b与y轴交于点A(0,7),直线l2:y=3x﹣3交y轴于点B,交直线l1于点P(2,m).

(1)求直线l1的解析式;
(2)求△PAB的面积.
相关试题

