【题目】如图,在数轴上A点表示数﹣3,B点表示数9,若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以3个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,则经过 秒,甲球到原点的距离等于乙球到原点的距离的两倍.
![]()
参考答案:
【答案】![]() 或
或![]() .
.
【解析】
试题分析:设经过t秒,甲球到原点的距离等于乙球到原点的距离的两倍.分两种情况:①0<t≤3,②t>3,根据甲球到原点的距离等于乙球到原点的距离的两倍列出关于t的方程,解方程即可.
解:设经过t秒,甲球到原点的距离等于乙球到原点的距离的两倍.
∵甲球运动的路程为:1t=t,OA=3,
∴甲球与原点的距离为:t+3;
乙球到原点的距离分两种情况:当0<t≤3时,乙球从点B处开始向左运动,一直到原点O,
∵OB=9,乙球运动的路程为:3t=3t,乙到原点的距离:9﹣3t(0≤t≤3);
当t>3时,乙球从原点O处开始一直向右运动,此时乙球到原点的距离为:3t﹣9 (t>3).
分两种情况:
①当0<t≤3时,得t+3=2(9﹣3t),解得t=![]() ;
;
当t>3时,得t+3=2(3t﹣9),解得t=![]() .
.
故当t=![]() 或
或![]() 秒时,甲球到原点的距离等于乙球到原点的距离的两倍.
秒时,甲球到原点的距离等于乙球到原点的距离的两倍.
故答案为:![]() 或
或![]() .
.
-
科目: 来源: 题型:
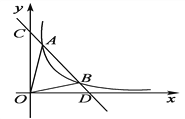
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
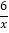 (x>0)的图象交于A(m,6),B(3,n)两点.
(x>0)的图象交于A(m,6),B(3,n)两点.(1)求一次函数的解析式;
(2)根据图象直接写出kx+b-
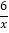 <0时x的取值范围;
<0时x的取值范围;(3)求△AOB的面积.
-
科目: 来源: 题型:
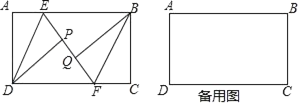
查看答案和解析>>【题目】如图,在矩形ABCD中,AD=4,E,F分别为边AB,CD上一动点,AE=CF,分别以DE,BF为对称轴翻折△ADE,△BCF,点A,C的对称点分别为P,Q.若点P,Q,E,F恰好在同一直线上,且PQ=1,则EF的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小莉的爸爸买了今年七月份去上海看世博会的一张门票,她和哥哥两人都很想去观看,可门票只有一张,读九年级的哥哥想了一个办法,拿了八张扑克牌,将数字为1,2,3,5的四张牌给小莉,将数字为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小莉和哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张扑克牌数字相加,如果和为偶数,则小莉去;如果和为奇数,则哥哥去.
(1)请用数状图或列表的方法求小莉去上海看世博会的概率;
(2)哥哥设计的游戏规则公平吗?若公平,请说明理由;若不公平,请你设计一种公平的游戏规则.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校初一(2)班组织学生从A地到B地步行野营,匀速前进,该班师生共56人,每8人排成一排,相邻两排之间间隔1米,途中经过一座桥CD,队伍从开始上桥到刚好完全离开桥共用了150秒,当队尾刚好走到桥的一端D处时,排在队尾的游班长发现小蒋还在桥的另一端C处拍照,于是以队伍1.5倍的速度返回去找小萍,同时队伍仍按原速度继续前行,30秒后,小蒋发现游班长返回来找他,便立刻以2.1米/秒的速度向游班长方向行进,小蒋行进40秒后与游班长相遇,相遇后两人以队伍2倍的速度前行追赶队伍.
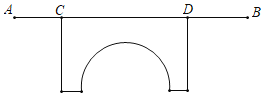
(1)初一(2)班的队伍长度为 米;
(2)求班级队伍行进的速度(列一元一次方程解决问题);
(3)请问:游班长从D处返回赵小萍开始到他们两人追上队首的刘老师一共用了多少时间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD交AC于点E,点O是AB上一点,⊙O过B、E两点,交BD于点G,交AB于点F.
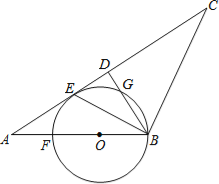
(1)判断直线AC与⊙O的位置关系,并说明理由;
(2)当BD=6,AB=10时,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,甲乙两点沿着边长为3cm的正方形,按A→B→C→D→A…的方向行走,甲从A点以3cm/s的速度、乙从B点以a cm/s的速度同时行走,设运动时间为t秒,t=2时甲乙两点第一次相遇.
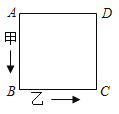
(1)求a
(2)若a>3,且甲乙第一次相遇后,乙的速度变为5cm/s,当两点第二次相遇前相距4cm时,t为多少?
相关试题

