【题目】在ΔABC中,∠ABC的平分线与∠ACB的外角∠ACE的平分线相交于点D。

⑴.若∠ABC=60°,∠ACB=40°,求∠A和∠D的度数。
⑵.由⑴小题的计算结果,猜想,∠A和∠D有什么数量关系,并加以证明。
参考答案:
【答案】(1)∠A=80°,∠D=40°;(2)∠A=2∠D,理由见解析
【解析】
(1)根据三角形内角和定理,已知∠ABC=60°,∠ACB=40°,易求∠A,根据角平分线定义和外角的性质即可求得∠D度数.
(2)根据三角形内角和定理以及角平分线性质,先求出∠D的等式,再与∠A比较即可解答.
(1)在△ABC中,∠ABC=60°,∠ACB=40°,
∴∠A=180°∠ABC∠ACB=80°,
∵BD为∠ABC,CD为∠ACE的角平分线,
∴∠DBC=![]() ∠ABC=
∠ABC=![]() ×60°=30°,
×60°=30°,
∠ACD=![]() (180°∠ACB)=
(180°∠ACB)=![]() ×140°=70°,
×140°=70°,
∴∠D=180°∠DBC∠ACB∠ACD=180°30°40°70°=40°,
∴∠A=80°,∠D=40°;
(2)通过第(1)的计算,得到∠A=2∠D,理由如下:
∵∠ACE=∠A+∠ABC,
∴∠ACD+∠ECD=∠A+∠ABD+∠DBE,∠DCE=∠D+∠DBC,
又∵BD平分∠ABC,CD平分∠ACE,
∴∠ABD=∠DBE,∠ACD=∠ECD,
∴∠A=2(∠DCE∠DBC),∠D=∠DCE∠DBC,
∴∠A=2∠D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求下列各数的算术平方根和平方根:
(1)900 (2)1 (3)
 (4)14 (5)
(4)14 (5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.

(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某农场有A、B两种型号的收割机共20台,每台A型收割机每天可收大麦100亩或者小麦80亩,每台B型收割机每天可收大麦80亩或者小麦60亩,该农场现有19 000亩大麦和11 500亩小麦先后等待收割.先安排这20台收割机全部收割大麦,并且恰好10天时间全部收完.
(1)问A、B两种型号的收割机各多少台?
(2)由于气候影响,要求通过加班方式使每台收割机每天多完成10%的收割量,问这20台收割机能否在一周时间内完成全部小麦收割任务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
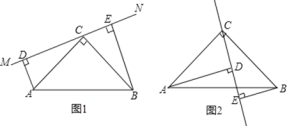
(1)求证:①△ADC≌△CEB;②DE=AD+BE.
(2)当直线MN绕点C旋转到图2的位置时,DE、AD、BE又怎样的关系?并加以证明.
-
科目: 来源: 题型:
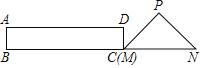
查看答案和解析>>【题目】如图,在Rt△PMN中,∠P=90°,PM=PN,MN=6cm,矩形ABCD中AB=2cm,BC=10cm,点C和点M重合,点B、C(M)、N在同一直线上,令Rt△PMN不动,矩形ABCD沿MN所在直线以每秒1cm的速度向右移动,至点C与点N重合为止,设移动x秒后,矩形ABCD与△PMN重叠部分的面积为y,则y与x的大致图象是( )
A.
 B.
B.  C.
C. 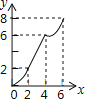 D.
D. 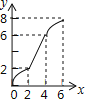
相关试题

