【题目】已知:在⊙O中,弦AC⊥弦BD,垂足为H,连接BC,过点D作DE⊥BC于点E,DE交AC于点F.
(1)如图1,求证:BD平分∠ADF;
(2)如图2,连接OC,若OC平分∠ACB,求证:AC=BC;
(3)如图3,在(2)的条件下,连接AB,过点D作DN∥AC交⊙O于点N,若tan∠ADB=![]() ,AB=3
,AB=3![]() ,求DN的长.
,求DN的长.



参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)9.
【解析】试题分析:(1)先根据同角的余角相等可证得: ∠ACB=∠BDE,再根据同弧所对的圆周角相等可得: ∠ACB=∠ADB,所以∠BDE=∠ADB,所以BD平分∠ADF,(2)连接OB,OA,则
△AOC,△BOC是等腰三角形,再证△AOC≌△BOC,根据全等三角形的性质可得:AC=BC,
(3)根据∠ACB=∠ADB, tan∠ADB=![]() ,所以tan∠ACB=
,所以tan∠ACB=![]() ,所以
,所以![]() ,可设BH=3x,CH=4x,由勾股定理可得:BC=5x,则AC=5x,所以AH=x,根据勾股定理可得:
,可设BH=3x,CH=4x,由勾股定理可得:BC=5x,则AC=5x,所以AH=x,根据勾股定理可得: ![]() ,因为AB=
,因为AB=![]() ,所以可得:
,所以可得: ![]() ,
,![]() ,解得:x=3,所以DH=4,CH=12,BH=9,BC=15,
,解得:x=3,所以DH=4,CH=12,BH=9,BC=15,
所以BD=13,由相似三角形性质可得:BN=![]() ,再根据勾股定理解得: DN=9.
,再根据勾股定理解得: DN=9.
试题解析:(1) 因为弦AC⊥弦BD, DE⊥BC于点E,
所以∠ACB+∠DBE=∠BDE+∠DBE=90°,
所以∠ACB=∠BDE,
又因为∠ACB=∠ADB,
所以∠BDE=∠ADB,
所以BD平分∠ADF,
(2) 连接OB,OA,则△AOC,△BOC是等腰三角形,
所以∠OCB=∠OBC, ∠OAC=∠OCA,
又因为OC平分∠ACB,
所以∠OCB==∠OCA,
所以∠OBC=∠OAC,
在△AOC和△BOC中,
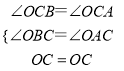 ,
,
所以△AOC≌△BOC,
所以AC=BC,
(3)因为∠ACB=∠ADB, tan∠ADB=![]() ,
,
所以tan∠ACB=![]() ,所以
,所以![]() ,可设BH=3x,CH=4x,由勾股定理得:BC=5x,
,可设BH=3x,CH=4x,由勾股定理得:BC=5x,
则AC=5x,所以AH=x,
因为AB=![]() ,根据勾股定理得:
,根据勾股定理得: ![]() ,
,
所以得: ![]() ,
,![]() ,解得:x=3,
,解得:x=3,
所以BC=15,
设等腰△ACB底边AB上的高为h,由勾股定理可得: ![]() ,
,
根据相似三角形性质可得: ![]() ,即
,即 ,解得BN=
,解得BN=![]() ,
,
根据勾股定理可得:DN=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机抽取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下:

根据上述信息完成下列问题:
(1)求本次调查共抽取了多少份书法作品?
(2)请在图②中把条形统计图补充完整;
(3)已知该校这次活动共收到参赛作品750份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的周长为29,一边长为7,则此等腰三角形的腰长为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点P在第二象限,它到x轴,y轴的距离分别为3,1,则点P的坐标为( )
A.(1,3)B.(﹣3,1)C.(﹣1,3)D.(3,﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是等边三角形
是等边三角形 内的一点,连结
内的一点,连结 、
、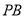 、
、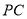 ,以
,以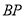 为边作
为边作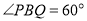 且
且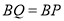 .连结
.连结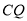 .
.(1)观察并猜想
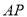 与
与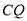 之间的大小关系,并证明你的结论.
之间的大小关系,并证明你的结论.(2)若
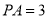 ,
, 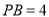 ,
, 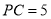 ,连结
,连结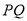 ,试判断
,试判断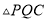 的形状,并说明理由.
的形状,并说明理由.(3)在(2)的条件下,求
 的面积.
的面积.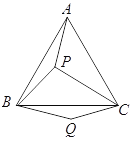
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:
(1)4a3﹣a;
(2)9+6(a+b)+(a+b)2;
(3)﹣8ax2+16axy﹣8ay2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品批发商场共用22000元同时购进A、B两种型号背包各400个,购进A型号背包30个比购进B型背包15个多用300元.
(1)求A、B两种型号背包的进货单价各为多少元?
(2)若商场把A、B两种型号背包均按每个50元定价进行零售,同时为扩大销售,拿出一部分背包按零售价的7折进行批发销售.商场在这批背包全部售完后,若总获利超过10500元,则商场用于批发的背包数量最多为多少个?
相关试题

