【题目】如图,已知A(0,a),B(0,b),C(m,b)且(a-4)2+|b+3|=0,S△ABC=14。

(1)求C点的坐标
(2)作DE⊥DC交y轴于E点,EF为∠AED的平分线,且∠DFE=90o。求证:FD平分∠ADO.
参考答案:
【答案】(1)(4,-3);(2)见解析;
【解析】
(1)根据平方根的性质和绝对值的非负性,求出a,b的值,再根据三角形面积公式即可解答.
(2)根据角平分线的性质,三角形的内角和定理,分别求出∠OEG=∠FDG和∠ADF=∠AEF即可求证.
(1)∵(a-4)2+|b+3|=0,
∴a=4,b=-3.
又∵S△ABC =14,
∴![]() × AB×BO=14,
× AB×BO=14,
∵AB=7
∴BC=4,C点的坐标为(4,-3);
(2)设OD与EF相交于点G,

∵∠F=90°,∠EOG=90°,
∴∠EGO=∠FGD,
∴∠OEG=∠FDG①,
∵∠ADE=90°,
∴∠ADF+∠FDE=90°,在△EFD中,∠FDE+∠FED=90°,
∴∠ADF=∠FED,
又∵EF平分∠AED,
∴∠AEF=∠FED,∴∠ADF=∠AEF②,
由①②得∠FDG=∠ADF,
∴FD平分∠ADO.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=
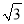 :3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:
:3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据: 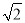 ≈1.414,
≈1.414, 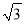 ≈1.732)
≈1.732)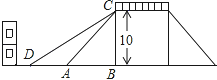
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
数学课上,老师给出了如下问题:
如图,AD为△ABC中线,点E在AC上,BE交AD于点F,AE=EF.求证:AC=BF.
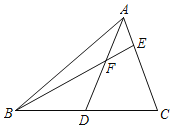
经过讨论,同学们得到以下两种思路:
思路一如图①,添加辅助线后依据SAS可证得△ADC≌△GDB,再利用AE=EF可以进一步证得∠G=∠FAE=∠AFE=∠BFG,从而证明结论.
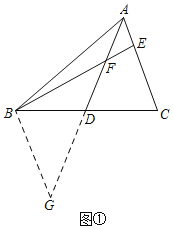
思路二如图②,添加辅助线后并利用AE=EF可证得∠G=∠BFG=∠AFE=∠FAE,再依据AAS可以进一步证得△ADC≌△GDB,从而证明结论.
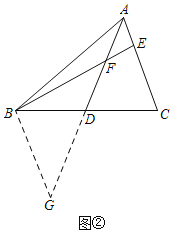
完成下面问题:
(1)①思路一的辅助线的作法是: ;
②思路二的辅助线的作法是: .
(2)请你给出一种不同于以上两种思路的证明方法(要求:只写出辅助线的作法,并画出相应的图形,不需要写出证明过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,王老师站在湖边度假村的景点A处,观察到一只水鸟由岸边D处飞向湖中小岛C处,点A到DC所在水平面的距离AB是15米,观测水鸟在点D和点C处时的俯角分别为53°和11°,求C、D两点之间距离.(精确到0.1.参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.33,sin11°≈0.19,cos11°≈0.98,tan11°≈0.19)

-
科目: 来源: 题型:
查看答案和解析>>【题目】随着智能分拣设备在快递业务中的普及,快件分拣效率大幅提高.使用某品牌智能分拣设备,每人每小时分拣的快件量是传统分拣方式的25倍,经过测试,由5人用此设备分拣8000件快件的时间,比20人用传统方式分拣同样数量的快件节省4小时.某快递中转站平均每天需要分拣10万件快件,如果使用此智能分拣设备,每天只需要安排多少名工人就可以完成分拣工作(每天工作时间为8小时).
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)6+(﹣
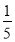 )﹣2﹣(﹣1.5)
)﹣2﹣(﹣1.5)(2)10+[
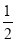 ﹣(﹣1+1
﹣(﹣1+1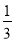 )]×6
)]×6(3)﹣2÷
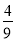 ×(
×(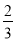 )2
)2(4)﹣32﹣|﹣6|﹣3×(﹣
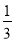 )+(﹣2)2÷
)+(﹣2)2÷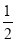
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某翼装飞行员从离水平地面高AC=500m的A处出发,沿着俯角为15°的方向,直线滑行1600米到达D点,然后打开降落伞以75°的俯角降落到地面上的B点.求他飞行的水平距离BC(结果精确到1m).

相关试题

