【题目】阅读下面材料:
数学课上,老师给出了如下问题:
如图,AD为△ABC中线,点E在AC上,BE交AD于点F,AE=EF.求证:AC=BF.
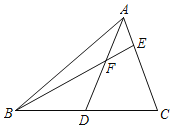
经过讨论,同学们得到以下两种思路:
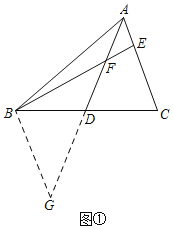
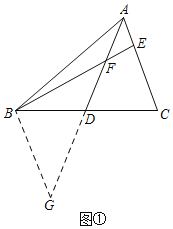
思路一如图①,添加辅助线后依据SAS可证得△ADC≌△GDB,再利用AE=EF可以进一步证得∠G=∠FAE=∠AFE=∠BFG,从而证明结论.
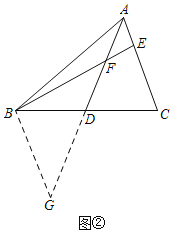
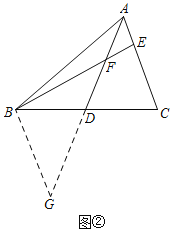
思路二如图②,添加辅助线后并利用AE=EF可证得∠G=∠BFG=∠AFE=∠FAE,再依据AAS可以进一步证得△ADC≌△GDB,从而证明结论.
完成下面问题:
(1)①思路一的辅助线的作法是: ;
②思路二的辅助线的作法是: .
(2)请你给出一种不同于以上两种思路的证明方法(要求:只写出辅助线的作法,并画出相应的图形,不需要写出证明过程).
参考答案:
【答案】(1)①延长AD至点G,使DG=AD,连接BG;②作BG=BF交AD的延长线于点G;(2)详见解析
【解析】
(1)①依据SAS可证得△ADC≌△GDB,再利用AE=EF可以进一步证得∠G=∠FAE=∠AFE=∠BFG,从而证明结论.
②作BG=BF交AD的延长线于点G.利用AE=EF可证得∠G=∠BFG=∠AFE=∠FAE,再依据AAS可以进一步证得△ADC≌△GDB,从而证明结论.
(2)作BG∥AC交AD的延长线于G,证明△ADC≌△GDB(AAS),得出AC=BG,证出∠G=∠BFG,得出BG=BF,即可得出结论.
解:(1)①延长AD至点G,使DG=AD,连接BG,如图①,理由如下:
∵AD为△ABC中线,
∴BD=CD,
在△ADC和△GDB中,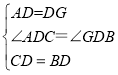 ,
,
∴△ADC≌△GDB(SAS),
∴AC=BG,
∵AE=EF,
∴∠CAD=∠EFA,
∵∠BFG=∠G,∠G=∠CAD,
∴∠G=∠BFG,
∴BG=BF,
∴AC=BF.
故答案为:延长AD至点G,使DG=AD,连接BG;
②作BG=BF交AD的延长线于点G,如图②.
理由如下:∵BG=BF,
∴∠G=∠BFG,
∵AE=EF,
∴∠EAF=∠EFA,
∵∠EFA=∠BFG,
∴∠G=∠EAF,
在△ADC和△GDB中,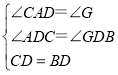 ,
,
∴△ADC≌△GDB(AAS),
∴AC=BG,
∴AC=BF;
故答案为:作BG=BF交AD的延长线于点G;
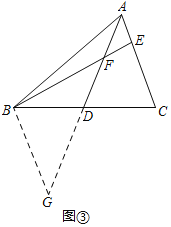
(2)作BG∥AC交AD的延长线于G,如图③所示:
则∠G=∠CAD,
∵AD为△ABC中线,
∴BD=CD,
在△ADC和△GDB中,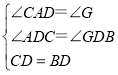 ,
,
∴△ADC≌△GDB(AAS),
∴AC=BG,
∵AE=EF,
∴∠CAD=∠EFA,
∵∠BFG=∠EFA,∠G=∠CAD,
∴∠G=∠BFG,
∴BG=BF,
∴AC=BF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请从以下两个小题中任选一题作答,若多选,则按第一题计分.
(A)儿童节期间,文具商店搞促销活动,同时购买一个书包和一个文具盒可以打8折优惠,能比标价省13.2元,已知书包标价比文具盒标价的3倍少6元.那么设一个文具盒标价为x元,依据题意列方程得________.
(B)用科学记算器计算:
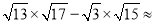 ________(计算结果保留两位小数).
________(计算结果保留两位小数). -
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图,△A1B1C1是△ABC向右平移四个单位长度后得到的,且三个顶点的坐标分别为A1(1,1),B1(4,2),C1(3,4).

(1)请画出△ABC,并写出点A、B、C的坐标;
(2)求出△AOA1的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=
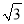 :3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:
:3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据: 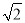 ≈1.414,
≈1.414, 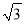 ≈1.732)
≈1.732)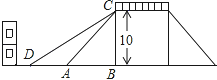
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,王老师站在湖边度假村的景点A处,观察到一只水鸟由岸边D处飞向湖中小岛C处,点A到DC所在水平面的距离AB是15米,观测水鸟在点D和点C处时的俯角分别为53°和11°,求C、D两点之间距离.(精确到0.1.参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.33,sin11°≈0.19,cos11°≈0.98,tan11°≈0.19)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(0,a),B(0,b),C(m,b)且(a-4)2+|b+3|=0,S△ABC=14。

(1)求C点的坐标
(2)作DE⊥DC交y轴于E点,EF为∠AED的平分线,且∠DFE=90o。求证:FD平分∠ADO.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着智能分拣设备在快递业务中的普及,快件分拣效率大幅提高.使用某品牌智能分拣设备,每人每小时分拣的快件量是传统分拣方式的25倍,经过测试,由5人用此设备分拣8000件快件的时间,比20人用传统方式分拣同样数量的快件节省4小时.某快递中转站平均每天需要分拣10万件快件,如果使用此智能分拣设备,每天只需要安排多少名工人就可以完成分拣工作(每天工作时间为8小时).
相关试题

