【题目】如图,点O是直线AB上一点,射线OA1 , OA2均从OA的位置开始绕点O顺时针旋转,OA1旋转的速度为每秒30°,OA2旋转的速度为每秒10°.当OA2旋转6秒后,OA1也开始旋转,当其中一条射线与OB重合时,另一条也停止.设OA1旋转的时间为t秒.
(1)用含有t的式子表示∠A1OA=°,∠A2OA=°;
(2)当t = , OA1是∠A2OA的角平分线;
(3)若∠A1OA2=30°时,求t的值.
参考答案:
【答案】
(1)30t;10(t+6)
(2)1.2
(3)
解:①当OA1在∠AOA2的内部时
10(t+6)- 30t = 30
解得 t=1.5
②当OA1在∠AOA2的外部时
30t - 10(t+6)= 30
解得 t=4.5
所以t为1.5或4.5.
答:t的值为1.5或4.5.
【解析】(1)利用速度![]() 时间,分别得出∠A1OA和∠A2OA的度数即可.
时间,分别得出∠A1OA和∠A2OA的度数即可.
(2)若OA1是∠A2OA的角平分线,则有∠A2OA=2∠A1OA,即10(t+6)=2![]() 30t,解得t =1.2.
30t,解得t =1.2.
(3)此问注意分情况讨论,分①当OA1在∠AOA2的内部时和 ②当OA1在∠AOA2的外部时两种情况.
【考点精析】通过灵活运用角的运算,掌握角之间可以进行加减运算;一个角可以用其他角的和或差来表示即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在徒骇河观景堤坝上有一段斜坡,为了方便游客通行,现准备铺上台阶,某施工队测得斜坡上铅锤的两棵树间水平距离AB=4米,斜坡距离BC=4.25米,斜坡总长DE=85米.
(1)求坡角∠D的度数(结果精确到1°)
(2)若这段斜坡用厚度为15cm的长方体台阶来铺,需要铺几级台阶?(最后一个高不足15cm时,按一个台阶计算)
(参考数据:cos20°≈0.94,sin20°≈0.34,sin18°≈0.31,cos18°≈0.95)
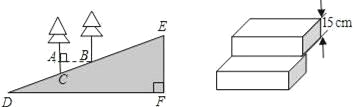
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=2,D是AB边上的一个动点(不与点A、B重合),过点D作CD的垂线交射线CA于点E.设AD=x,CE=y,则下列图象中,能表示y与x的函数关系图象大致是( )
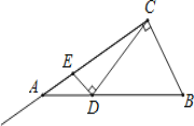
A.
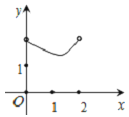 B.
B. 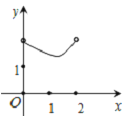 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】若am=2,an=8,则am+n= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣1)2n+(﹣1)2n+1的值是( )
A.2
B.﹣2
C.±2
D.0 -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
数轴的方向和单位长度都不变,只移动原点的位置,这种数轴的变换叫做数轴的平移.已知数轴上的点A表示数-3,点B表示数6.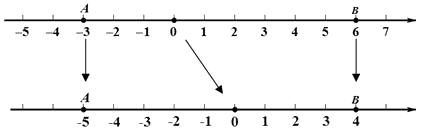
(1)探究:如图,把原点移到表示数2的点上,点A表示的新数为-5,点B表示的新数为4.把原点移到表示数-1的点上,点A表示的新数为 , B表示的新数为.
(2)归纳:把原点移到表示数a的点上,点A,B表示的新数分别为 , .(用含a的式子表示);
(3)应用:①如果点C表示数是12,经过数轴的平移变换,表示的新数为7,那么原点移动到
表示数的点上;
②如果点D表示数为x,当原点移到表示数-1的点上时,点D表示的新数为 x, 则x =;
x, 则x =;
(4)拓展:平移数轴,把原点移动到表示数a的点P上,若PA:PB=4:5,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙).那么通过计算两个图形阴影部分的面积,可以验证成立的公式为( )

A.a2﹣b2=(a﹣b)2
B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=a2﹣2ab+b2
D.a2﹣b2=(a+b)(a﹣b)
相关试题

