【题目】鸡年春节前夕,海春中学向全校3000名学生发出“减少空气污染,少放烟花炮竹”倡议书,春节后随机抽取100名学生进行问卷调查,问卷选项有四项:A.自己没有燃放烟花炮竹;B.在规定时间和规定地点少量燃放烟花炮竹;C.随意燃放烟花炮竹;D.不仅自己不燃放同时劝阻身边亲友不燃放烟花炮竹.并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答以下问题:
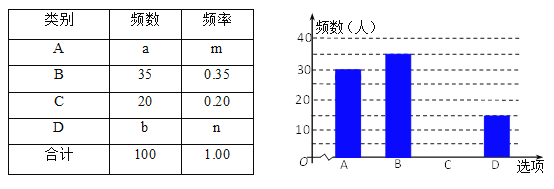
(1)表格中a= ,b= ,并补全条形统计图;
(2)如果绘制扇形统计图,请求出C类所占的圆心角的度数;
(3)根据抽样结果,请估计全校“自己没有燃放烟花炮竹”和“不仅自己不燃放同时劝阻身边亲友不燃放烟花炮竹”的学生共有多少名?
参考答案:
【答案】(1)30,15,补图见解析;(2)C类圆心角的度数为72°;(3)1350名.
【解析】试题分析:(1)根据图示和列表直接求出a、b的值,然后补图即可;
(2)根据C的人数占总人数的百分比乘以360°即可;
(3)求出A、D的人数和占总人数的百分比,乘以总数即可.
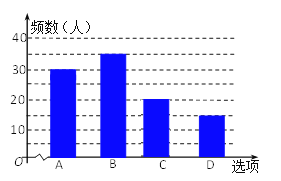
试题解析:(1)30,15,补图如下:
(2)C类圆心角的度数为![]() ;
;
(3)(30+15)÷100×3000=1350(名)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形具有稳定性的是( )
A. 三角形 B. 四边形 C. 五边形 D. 六边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点P(﹣2,b)与点M(a,3)关于原点对称,则a+b=_____.
-
科目: 来源: 题型:
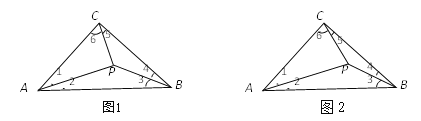
查看答案和解析>>【题目】如图1,已知:在△ABC中,∠ACB=90°,AC=BC,△ABC内一点P将三个内角分成6个角(即∠1、∠2、∠3、∠4、∠5、∠6).
(1)若∠1=∠3=∠5,求
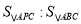 的值;
的值;(2)如图2,已知:AP=AC.
①若PB=PC,求证:∠1=2∠4;
②若∠1=30°,求证:PB=PC.
-
科目: 来源: 题型:
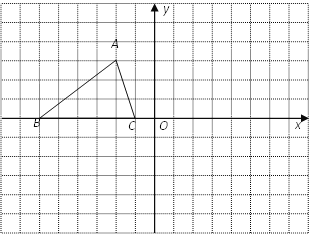
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点
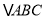 (顶点是网格线的交点),已知
(顶点是网格线的交点),已知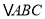 三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).(1)经过怎样的平移,可使
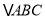 的顶点A与坐标原点O重合,画出平移后的三角形△
的顶点A与坐标原点O重合,画出平移后的三角形△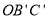 ;
;(2)已知△
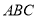 的重心G的坐标为
的重心G的坐标为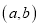 ,请直接写出△
,请直接写出△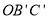 的重心
的重心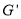 的坐标(分别用
的坐标(分别用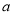 、
、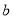 的代数式表示);
的代数式表示);(3)将
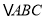 绕坐标原点
绕坐标原点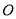 逆时针旋转90°,得到△
逆时针旋转90°,得到△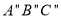 ,画出△
,画出△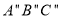 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数据:﹣1,4,2,﹣2,x的众数是2,那么这组数据的平均数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是“赵爽弦图”,其中△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABC的和EFGH都是正方形.根据这个图形的面积关系,可以证明勾股定理.设AD=c,AE=b,c=10,a﹣b=2.
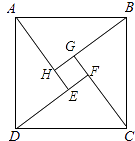
(1)正方形EFGH的面积为 , 四个直角三角的面积和为 .
(2)求(a+b)2的值.
(3)a+b= , a= , b= .
相关试题

