【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:
①abc>0;②9a+3b+c<0;③c>﹣1;④关于x的方程ax2+bx+c=0(a≠0)有一个根为﹣ ![]()
其中正确的结论个数有( )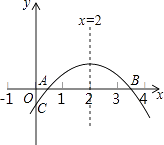
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】C
【解析】解:
由图象开口向下,可知a<0,
与y轴的交点在x轴的下方,可知c<0,
又对称轴方程为x=2,所以﹣ ![]() >0,所以b>0,
>0,所以b>0,
∴abc>0,故①正确;
由图象可知当x=3时,y>0,
∴9a+3b+c>0,故②错误;
由图象可知OA<1,
∵OA=OC,
∴OC<1,即﹣c<1,
∴c>﹣1,故③正确;
假设方程的一个根为x=﹣ ![]() ,把x=﹣
,把x=﹣ ![]() 代入方程可得
代入方程可得 ![]() ﹣
﹣ ![]() +c=0,
+c=0,
整理可得ac﹣b+1=0,
两边同时乘c可得ac2﹣bc+c=0,
即方程有一个根为x=﹣c,
由②可知﹣c=OA,而当x=OA是方程的根,
∴x=﹣c是方程的根,即假设成立,故④正确;
综上可知正确的结论有三个,
故答案为:C.
抛物线开口由a决定,9a+3b+c可由x=3时的函数值看出,由OA=OC可知OA=-c,由图像知ax2+bx+c=0(a≠0)有一个根为-c,由根与系数关系得-c![]() x2=
x2=![]() ,另一个根为
,另一个根为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知⊙A经过点E,B,C,O,且C(0,6)、E(﹣8,0)、O(0,0),则cos∠OBC的值为( )
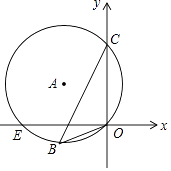
A.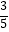
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=2
 ,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF
,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF
(1)如图1,求证:AE=CF;
(2)如图2,若A,E,O三点共线,求点F到直线BC的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )

A. OE=
 DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是用直尺和圆规作一个角等于己知角的方法,即作
 .这种作法依据的是( )
.这种作法依据的是( )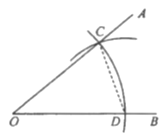
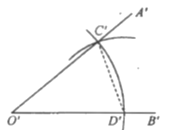
A.SSSB.SASC.AASD.ASA
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(2,m)是第一象限内一点,连接OA,将OA绕点A逆时针旋转90°得到线段AB,若反比例函数y=
 (x>0)的图象恰好同时经过点A、B,则k的值为 .
(x>0)的图象恰好同时经过点A、B,则k的值为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 中,
中, ,点
,点 在边
在边 上,且
上,且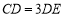 ,将
,将 沿
沿 对折至
对折至 ,延长
,延长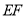 交边
交边 于点
于点 ,连接
,连接 ,
, ,则下列结论:①
,则下列结论:① ≌
≌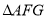 ;②
;② ;③
;③ ;④
;④ ,其中正确的个数是( )个
,其中正确的个数是( )个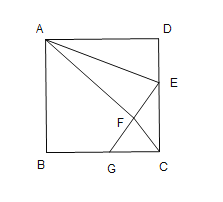
A.1B.2C.3D.4
相关试题

