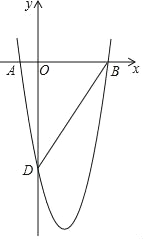
【题目】如图,二次函数y=ax2+bx﹣4![]() 的图象经过A(﹣1,0)、B(4,0)两点,于y轴交于点D.
的图象经过A(﹣1,0)、B(4,0)两点,于y轴交于点D.
(1)求这个二次函数的表达式;
(2)已知点C(3,m)在这个二次函数的图象上,连接BC,点P为抛物线上一点,且∠CBP=60°.
①求∠OBD的度数;
②求点P的坐标.
参考答案:
【答案】(1)二次函数的表达式为y=![]() x2﹣3
x2﹣3![]() x﹣4
x﹣4![]() ;(2)①60°,②(-
;(2)①60°,②(-![]() ,
,![]() )
)
【解析】分析:(1)代入A、B点坐标即可求得a、b的值,即可解题;
(2)①易证△BOD是含30°角的直角三角形,即可解题;
②过点P作PE⊥x轴于点E,过点C作CF⊥BD于点F,易证△CBF∽△PBE,可得![]() ,即可解题.
,即可解题.
详解:(1)由题意知:![]() ,解得
,解得![]() .
.
∴该二次函数的表达式为y=![]() x2﹣3
x2﹣3![]() x﹣4
x﹣4![]() ;
;
(2)①∵当x=0时,y=﹣4![]() .
.
∴抛物线与y轴交点D的坐标为(0,﹣4![]() ).
).
∵在△BOD中,∠BOD=90°,OB=4,OD=4![]() ,
,
∴BD=![]() =8,即BD=2OB,
=8,即BD=2OB,
∴∠ODB=30°.
∴∠OBD=60°;
②过点P作PE⊥x轴于点E,过点C作CF⊥BD于点F,
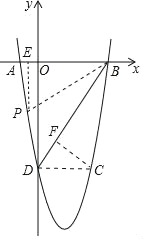
∵x=3时,m=﹣4![]() .
.
∴点C的坐标为(3,﹣4![]() ).
).
∵CD∥x轴,
∴CD=3,∠CDB=60°,∠DCF=30°.
∴DF=![]() CD=
CD=![]() ,CF=
,CF=![]() ,
,
∵BD=8,
∴BF=8﹣![]() =
=![]() ,
,
设点P的坐标为(x,![]() x2﹣3
x2﹣3![]() x﹣4
x﹣4![]() ).
).
则PE=﹣![]() x2+3
x2+3![]() x+4
x+4![]() ,BE=4﹣x,
,BE=4﹣x,
∵∠CBP=∠OBD=60°,
∴∠CBF=∠PBE.
∵∠CFB=∠PEB=90°.
∴△CBF∽△PBE.
∴![]() .
.
∴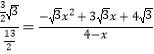 ,
,
解得:x1=4(舍去),x2=﹣![]() .
.
∵当x=﹣![]() 时,y=﹣
时,y=﹣![]() .
.
∴点P的坐标为(﹣![]() ,﹣
,﹣![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.分析甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分钟)变化的函数图象,解决下列问题:
(1)求出甲、乙两人所行驶的路程S甲、S乙与t之间的关系式;
(2)甲行驶10分钟后,甲、乙两人相距多少千米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,D为AB边上一点,连接CD,E为CD的中点,连接BE并延长至点F,使得EF=EB,连接DF交AC于点G,连接CF,
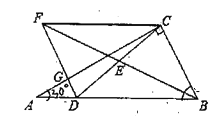
(1)求证:四边形DBCF是平行四边形
(2)若∠A=30°,BC=4,CF=6,求CD的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠ADC=90°,BC=8,DC=6,AD=10,动点P从点D出发,沿线段DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点P运动到点A时,点Q随之停止运动,设运动的时间为t(秒)。

(1)当点P运动t秒后,AP=____________(用含t的代数式表示);
(2)若四边形ABQP为平行四边形,求运动时间t;
(3)当t为何值时,△BPQ是以BQ或BP为底边的等腰三角形;
-
科目: 来源: 题型:
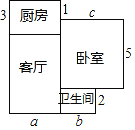
查看答案和解析>>【题目】小王家新买的一套住房的建筑平面图如图所示(单位:米).
(1)这套住房的建筑总面积是多少平方米?(用含a,b,c的式子表示)
(2)若a=9,b=4,c=7,试求出小王家这套住房的具体面积.
(3)地面装修要铺设瓷砖,公司报价是:客厅地面每平方米200元,卧室地面每平方米150元,厨房地面每平方米120元,卫生间地面每平方米100元.在(2)的条件下,小王一共要花多少钱?
(4)这套住房的售价为每平方米4500元,购房时首付款为房价的40%,余款向银行申请贷款,在(2)的条件下,小宇家购买这套住房时向银行申请贷款的金额是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字后,回答问题:
甲、乙两人同时解答题目:“化简并求值:
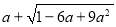 ,其中a=5.”甲、乙两人的解答不同;
,其中a=5.”甲、乙两人的解答不同;甲的解答是:
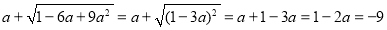 ;
;乙的解答是:
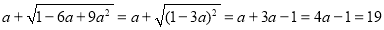 .
.(1) 的解答是错误的.
(2)错误的解答在于未能正确运用二次根式的性质: .
(3)模仿上题解答:化简并求值:
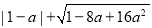 ,其中a=2.
,其中a=2. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了了解学生每周在校参加体育锻炼的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:


(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?
相关试题

