【题目】已知:在平面直角坐标系中,抛物线![]() 交x轴于A、B两点,交y轴于点C,且对称轴为x=﹣2,点P(0,t)是y轴上的一个动点.
交x轴于A、B两点,交y轴于点C,且对称轴为x=﹣2,点P(0,t)是y轴上的一个动点.

(1)求抛物线的解析式及顶点D的坐标.
(2)如图1,当0≤t≤4时,设△PAD的面积为S,求出S与t之间的函数关系式;S是否有最小值?如果有,求出S的最小值和此时t的值.
(3)如图2,当点P运动到使∠PDA=90°时,Rt△ADP与Rt△AOC是否相似?若相似,求出点P的坐标;若不相似,说明理由.
参考答案:
【答案】(1)y=﹣![]() (x+2)2+4,顶点D的坐标为(﹣2,4);(2)S=﹣2t+12,t=4时,S有最小值,最小值4;(3) 点P的坐标为(0,2).
(x+2)2+4,顶点D的坐标为(﹣2,4);(2)S=﹣2t+12,t=4时,S有最小值,最小值4;(3) 点P的坐标为(0,2).
【解析】(1)对称轴为x=﹣ =﹣2,
=﹣2,
解得b=﹣1,
所以,抛物线的解析式为y=﹣![]() x2﹣x+3,
x2﹣x+3,
∵y=﹣![]() x2﹣x+3=﹣
x2﹣x+3=﹣![]() (x+2)2+4,
(x+2)2+4,
∴顶点D的坐标为(﹣2,4);
(2)令y=0,则﹣![]() x2﹣x+3=0,
x2﹣x+3=0,
整理得,x2+4x﹣12=0,
解得x1=﹣6,x2=2,
∴点A(﹣6,0),B(2,0),
如图1,过点D作DE⊥y轴于E,
∵0≤t≤4,
∴△PAD的面积为S=S梯形AOED﹣S△AOP﹣S△PDE,
=![]() ×(2+6)×4﹣
×(2+6)×4﹣![]() ×6t﹣
×6t﹣![]() ×2×(4﹣t),
×2×(4﹣t),
=﹣2t+12,
∵k=﹣2<0,
∴S随t的增大而减小,
∴t=4时,S有最小值,最小值为﹣2×4+12=4;
(3)如图2,过点D作DF⊥x轴于F,
∵A(﹣6,0),D(﹣2,4),
∴AF=﹣2﹣(﹣6)=4,
∴AF=DF,
∴△ADF是等腰直角三角形,
∴∠ADF=45°,
由二次函数对称性,∠BDF=∠ADF=45°,
∴∠PDA=90°时点P为BD与y轴的交点,
∵OF=OB=2,
∴PO为△BDF的中位线,
∴OP=![]() DF=2,
DF=2,
∴点P的坐标为(0,2),
由勾股定理得,DP=![]() =2
=2![]() ,
,
AD=![]() AF=4
AF=4![]() ,
,
∴![]() =
=![]() =2,
=2,
令x=0,则y=3,
∴点C的坐标为(0,3),OC=3,
∴![]() =
=![]() =2,
=2,
∴![]() =
=![]() ,
,
又∵∠PDA=90°,∠COA=90°,
∴Rt△ADP∽Rt△AOC.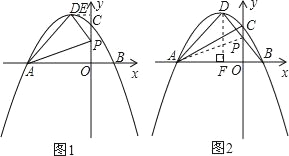
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式:①2a+b和a+b,②5m(a-b)和-a+b,③3(a+b)和-a-b,④x2-y2和x2+y2。其中有公因式的是( )
A.①② B.②③ C.③④ D.①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组
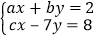 时,本应解出
时,本应解出 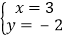 ,但由于看错了系数c , 而得到解为
,但由于看错了系数c , 而得到解为 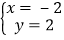 ,试求a+b+c的值.
,试求a+b+c的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】同一平面内的三条直线,其交点个数可能是( )
A. 0或3 B. 1或2或3
C. 0或1或2 D. 0或1或2或3
-
科目: 来源: 题型:
查看答案和解析>>【题目】某星期下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )

A.小强从家到公共汽车在步行了2公里
B.小强在公共汽车站等小明用了10分钟
C.公共汽车的平均速度是30公里/小时
D.小强乘公共汽车用了20分钟 -
科目: 来源: 题型:
查看答案和解析>>【题目】老师对甲、乙两人的五次数学测验成绩进行统计,得出两人五次测验成绩的平均分均为90分,方差分别是S甲2=51、S乙2=12.则成绩比较稳定的是( )
A. 甲B. 乙C. 两者相同D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】我校生物兴趣小组的学生,将自己收集的标本向本组其他成员各赠送一件,全组互赠182件,如果全组有x名同学,则根据题意列出的方程是( )
A.x(x+1)=182
B.x(x﹣1)=182
C.2x(x+1)=182
D.x(x﹣1)=182×2
相关试题

