搜索
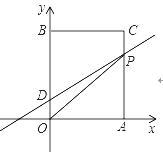
【题目】如图在平面直角坐标系中，O是坐标原点，矩形OACB的顶点A，B分别在x轴、y轴上，已知
，点D为y轴上一点，其坐标为
，若连接CD，则
，点P从点A出发以每秒1个单位的速度沿线段
的方向运动，当点P与点B重合时停止运动，运动时间为t秒
（1）求B，C两点坐标；
（2）求
的面积S关于t的函数关系式；
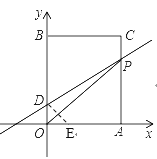
（3）当点D关于OP的对称点E落在x轴上时，请直接写出点E的坐标，并求出此时的t值．
参考答案：
【答案】（1）
，
（2）
（3）3
【解析】
（1）由勾股定理可确定BD长，即可依据题意写出B，C两点坐标；
（2）分情况讨论，当点P在AC上时，面积为一定值，直接求出即可，当点P在BC上时，以DO为底，BP为高，用含t的式子表示出BP即可得
的面积S关于t的函数关系式.
（3）当点D关于OP的对称点E落在x轴上时，此时OP垂直平分DE，故OE=OD=1，可知点E坐标，再证 
为等腰直角三角形即可确定t的值.
（1）
四边形OACB是矩形，
，
在
中，
，
，
，
，
，
；
（2）当点P在AC上时，
，，
；
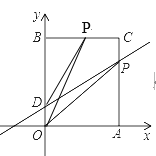
当点P在BC上时，，
，
；
（3）
，
当点D关于OP的对称落在x轴上时，
，
为等腰直角三角形，
，
.
-
科目： 来源： 题型：
查看答案和解析>>【题目】用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干个图案：第（4）个图案中有黑色地砖4块；那么第（n）个图案中有白色地砖________块
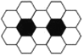
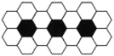
（1） （2） （3）
A.nB.6nC.
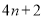D.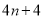
-
科目： 来源： 题型：
查看答案和解析>>【题目】每到春夏交替时节，雌性杨树会以满天飞絮的方式来传播下一代，漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等，给人们造成困扰，为了解市民对治理杨絮方法的赞同情况，某课题小组随机调查了部分市民（问卷调查表如表所示），并根据调查结果绘制了如下尚不完整的统计图．
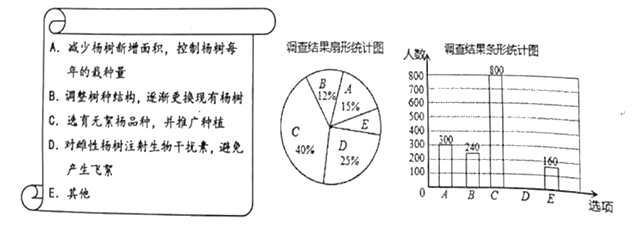
根据以上统计图，解答下列问题：
（1）求出本次接受调查的市民共有多少人？
（2）扇形统计图中，扇形E的圆心角度数是_________；
（3）请补全条形统计图；
（4）若该市约有80万人，请估计赞同“选育无絮杨品种，并推广种植”的人数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在
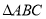中，按如下步骤作图：①以点A为圆心，AB长为半径画弧；
②以点C为圆心，CB长为半径画弧，两弧相交于点D；
③连接BD，与AC交于点E，连接AD、CD；
（1）求证：
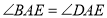；（2）当
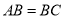时，猜想四边形ABCD是什么四边形，并证明你的结论；（3）当
，
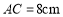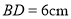，现将四边形ABCD通过割补，拼成一个正方形，那么这个正方形的边长是多少？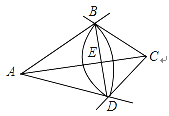
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系
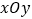中，△
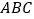的顶点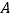
、
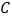在坐标轴上，点
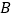的坐标是(2,2)．将△ABC沿
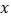轴向左平移得到△A1B1C1，点
落在函数y=-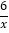
．如果此时四边形
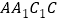的面积等于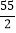
，那么点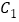
的坐标是________．
-
科目： 来源： 题型：
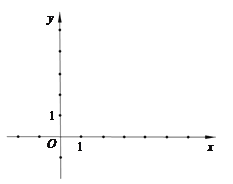
查看答案和解析>>【题目】如图，在平面直角坐标系
中，直线y=kx+3与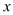
轴、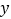
轴分别相交于点A、B，并与抛物线
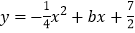的对称轴交于点
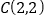，抛物线的顶点是点
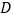．（1）求k和b的值；
（2）点G是
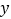轴上一点，且以点
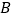、C、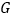
为顶点的三角形与△
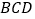相似，求点G的坐标；（3）在抛物线上是否存在点E：它关于直线AB的对称点F恰好在y轴上．如果存在，直接写出点E的坐标，如果不存在，试说明理由．
-
科目： 来源： 题型：
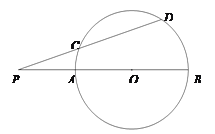
查看答案和解析>>【题目】已知P是
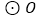的直径BA延长线上的一个动点，∠P的另一边交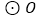于点C、D，两点位于AB的上方，
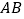＝6，OP=m，
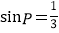，如图所示．另一个半径为6的
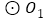经过点C、D，圆心距
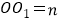．（1）当m=6时，求线段CD的长；
（2）设圆心O1在直线
上方，试用n的代数式表示m；（3）△POO1在点P的运动过程中，是否能成为以OO1为腰的等腰三角形，如果能，试求出此时n的值；如果不能，请说明理由．
相关试题
