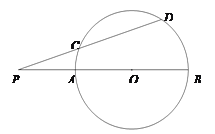
【题目】已知P是![]() 的直径BA延长线上的一个动点,∠P的另一边交
的直径BA延长线上的一个动点,∠P的另一边交![]() 于点C、D,两点位于AB的上方,
于点C、D,两点位于AB的上方,![]() =6,OP=m,
=6,OP=m,![]() ,如图所示.另一个半径为6的
,如图所示.另一个半径为6的![]() 经过点C、D,圆心距
经过点C、D,圆心距![]() .
.
(1)当m=6时,求线段CD的长;
(2)设圆心O1在直线![]() 上方,试用n的代数式表示m;
上方,试用n的代数式表示m;
(3)△POO1在点P的运动过程中,是否能成为以OO1为腰的等腰三角形,如果能,试求出此时n的值;如果不能,请说明理由.
参考答案:
【答案】(1)CD=![]() ;(2)m=
;(2)m=![]() ;(3) n的值为
;(3) n的值为![]() 或
或![]()
【解析】分析:(1)过点![]() 作
作![]() ⊥
⊥![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() .解Rt△
.解Rt△![]() ,得到
,得到![]() 的长.由勾股定理得
的长.由勾股定理得![]() 的长,再由垂径定理即可得到结论;
的长,再由垂径定理即可得到结论;
(2)解Rt△![]() ,得到
,得到![]() 和Rt△
和Rt△![]() 中,由勾股定理即可得到结论;
中,由勾股定理即可得到结论;
(3)△![]() 成为等腰三角形可分以下几种情况讨论:① 当圆心
成为等腰三角形可分以下几种情况讨论:① 当圆心![]() 、
、![]() 在弦
在弦![]() 异侧时,分
异侧时,分![]() 和
和![]() .②当圆心
.②当圆心![]() 、
、![]() 在弦
在弦![]() 同侧时,同理可得结论.
同侧时,同理可得结论.
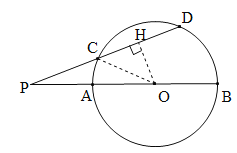
详解:(1)过点![]() 作
作![]() ⊥
⊥![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() .
.
在Rt△![]() ,∴
,∴![]() .
.
∵![]() =6,∴
=6,∴![]() .
.
由勾股定理得: ![]() .
.
∵![]() ⊥
⊥![]() ,∴
,∴![]() .
.
(2)在Rt△![]() ,∴
,∴![]() .
.
在Rt△![]() 中,
中,![]() .
.
在Rt△![]() 中,
中,![]() .
.
可得: ![]() ,解得
,解得![]() .
.
(3)△![]() 成为等腰三角形可分以下几种情况:
成为等腰三角形可分以下几种情况:
① 当圆心![]() 、
、![]() 在弦
在弦![]() 异侧时
异侧时
i)![]() ,即
,即![]() ,由
,由![]() ,解得
,解得![]() .
.
即圆心距等于![]() 、
、![]() 的半径的和,就有
的半径的和,就有![]() 、
、![]() 外切不合题意舍去.
外切不合题意舍去.
ii)![]() ,由
,由![]()
![]() ,
,
解得:![]() ,即
,即![]()
![]() ,解得
,解得![]() .
.
②当圆心![]() 、
、![]() 在弦
在弦![]() 同侧时,同理可得:
同侧时,同理可得: ![]() .
.
∵![]() 是钝角,∴只能是
是钝角,∴只能是![]() ,即
,即![]() ,解得
,解得![]() .
.
综上所述:n的值为![]() 或
或![]() .
.
-
科目: 来源: 题型:
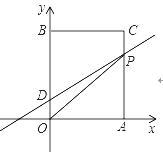
查看答案和解析>>【题目】如图在平面直角坐标系中,O是坐标原点,矩形OACB的顶点A,B分别在x轴、y轴上,已知
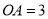 ,点D为y轴上一点,其坐标为
,点D为y轴上一点,其坐标为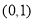 ,若连接CD,则
,若连接CD,则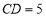 ,点P从点A出发以每秒1个单位的速度沿线段
,点P从点A出发以每秒1个单位的速度沿线段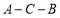 的方向运动,当点P与点B重合时停止运动,运动时间为t秒
的方向运动,当点P与点B重合时停止运动,运动时间为t秒(1)求B,C两点坐标;
(2)求
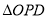 的面积S关于t的函数关系式;
的面积S关于t的函数关系式;(3)当点D关于OP的对称点E落在x轴上时,请直接写出点E的坐标,并求出此时的t值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,△
中,△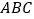 的顶点
的顶点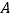 、
、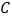 在坐标轴上,点
在坐标轴上,点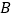 的坐标是(2,2).将△ABC沿
的坐标是(2,2).将△ABC沿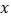 轴向左平移得到△A1B1C1,点
轴向左平移得到△A1B1C1,点 落在函数y=-
落在函数y=-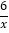 .如果此时四边形
.如果此时四边形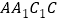 的面积等于
的面积等于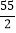 ,那么点
,那么点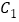 的坐标是________.
的坐标是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,直线y=kx+3与
中,直线y=kx+3与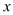 轴、
轴、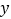 轴分别相交于点A、B,并与抛物线
轴分别相交于点A、B,并与抛物线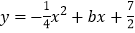 的对称轴交于点
的对称轴交于点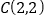 ,抛物线的顶点是点
,抛物线的顶点是点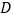 .
.(1)求k和b的值;
(2)点G是
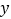 轴上一点,且以点
轴上一点,且以点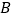 、C、
、C、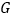 为顶点的三角形与△
为顶点的三角形与△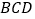 相似,求点G的坐标;
相似,求点G的坐标;(3)在抛物线上是否存在点E:它关于直线AB的对称点F恰好在y轴上.如果存在,直接写出点E的坐标,如果不存在,试说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点C在直线AB上,
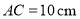 ,
,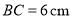 ,点M,N分别是AC,BC的中点,画出线段示意图并求线段MN的长.
,点M,N分别是AC,BC的中点,画出线段示意图并求线段MN的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下面三行数:
-3,9,-27,81,…;①
1,-3,9,-27,…;②
-1,11,-25,83,…;③
(1)第①行数按什么规律排列?第10个数是________;
(2)第②③行数与第①行数分别有什么关系?
(3)设x、y、z分别为第①②③行的第2018个数,求
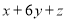 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】电话计费问题
下表中有两种移动电话计费方式方式
月使用费/元
主叫限定
时间/min
主叫超时
费/(元/min)
被叫
方式一
50
120
0.2
免费
方式二
80
300
0.1
免费
解决问题:
(1)设一个月内使用移动电话主叫时间为t分钟(为正整数).根据上表信息填写下表:
主叫时间t(分钟)
方式一计费(元)
方式二计费(元)
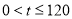
50
80
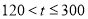
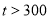
(2)如果王刚每月打电话的主叫时间t不超过500分钟,请你帮助他分析选择一种省钱的计费方式,并说明理由.
相关试题

