【题目】如图,正方形![]() 中,延长
中,延长![]() 至
至![]() 使
使![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() 分别与
分别与![]() ,
,![]() 交于点
交于点![]() .则下列说法:①
.则下列说法:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的有( )
.其中正确的有( )

A.4个B.3个C.2个D.1个
参考答案:
【答案】A
【解析】
根据正方形的性质,以及中点的性质可得△FGN≌△HAN,即证①;利用角度之间的等量关系的转换可以判断②;根据△AKH∽△MKF,进而利用相似三角形的性质即可判断③;设AN=![]() AG=x,则AH=2x,FM=6x,根据△AKH∽△MKF得出
AG=x,则AH=2x,FM=6x,根据△AKH∽△MKF得出![]() ,再利用三角形的面积公式求出△AFN的面积,再利用
,再利用三角形的面积公式求出△AFN的面积,再利用![]() 即可求出四边形DHKM的面积,作比即可判断④.
即可求出四边形DHKM的面积,作比即可判断④.
∵四边形EFGB是正方形,CE=2EB,四边形ABCD是正方形
∴G为AB中点,∠FGN=∠HAN=90°,AD=AB
即FG=AG=GB=![]() AB
AB
又H是AD的中点
AH=![]() AD
AD
∴FG=HA
又∠FNG=∠HNA
∴△FGN≌△HAN,故①正确;
∵∠DAM+∠GAM=90°
又∠NFG+∠FNG=90°
即∠FNG=∠GAM
∵∠FNG+∠NFG+90°=180°
∠AMD+∠DAM+90°=180°
∠FNG=∠GAM=∠AMD
∴![]() ,故②正确;
,故②正确;
由图可得:MF=FG+MG=3EB
△AKH∽△MKF
∴![]()
∴KF=3KH
又∵NH=NF
且FH=KF+KH=4KH=NH+NF
∴NH=NF=2KH
∴KH=KN
∴FN=2NK,故③正确;
∵AN=GN且AN+GN=AG
∴可设AN=![]() AG=x,则AH=2x,FM=6x
AG=x,则AH=2x,FM=6x
由题意可得:△AKH∽△MKF且相似比为:![]()
∴△AKH以AH为底边的高为:![]()
∴![]()
![]()
![]()
∴![]() ,故④正确;
,故④正确;
故答案选择A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用一张高为30
 ,宽为
,宽为 的长方形打印纸打印文档,如果左右的页边距都为
的长方形打印纸打印文档,如果左右的页边距都为 ,上下页边距比左右页边距多
,上下页边距比左右页边距多 .
.(1)请用
 的代数式表示中间打印部分的面积.
的代数式表示中间打印部分的面积.(2)当
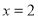 时,中间打印部分的面积是多少平方厘米?
时,中间打印部分的面积是多少平方厘米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料一:小明计算
 ,发现其结果为
,发现其结果为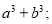 计算
计算 ,发现其结果为
,发现其结果为
阅读材料二:小华发现一个有趣的算式

(1)请模仿小华的算式,再写出一个类似的正确算式;
(2)请用字母表示小华算式的规律;
(3)请用阅读材料一中蕴含的数学规律或你掌握的数学知识说明(2)中的规律为何成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数y=k1x(k1≠0)与反比例函数
 的图象交于A、B两点,点A的坐标为(2,1).
的图象交于A、B两点,点A的坐标为(2,1). (1)求正比例函数、反比例函数的表达式;
(2)求点B的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为响应党的“文化自信”号召,某校开展了古诗词诵读大赛活动,现随机抽取部分同学的成绩进行统计,并绘制成如下的两个不完整的统计图,请结合图中提供的信息,解答下列各题:
(1)直接写出a的值,a= ,并把频数分布直方图补充完整.
(2)求扇形B的圆心角度数.
(3)如果全校有2000名学生参加这次活动,90分以上(含90分)为优秀,那么估计获得优秀奖的学生有多少人?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在某建筑物AC上,挂着一宣传条幅BC,站在点F处,测得条幅顶端B的仰角为300,往条幅方向前行20米到达点E处,测得条幅顶端B的仰角为600,求宣传条幅BC的长.(
 ,结果精确到0.1米)
,结果精确到0.1米)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,以
 的斜边
的斜边 为边,在
为边,在 的同侧作正方形
的同侧作正方形 ,
, ,
, 交于点
交于点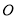 ,连接
,连接 .若
.若 ,
, ,则
,则 ________.
________.
相关试题

