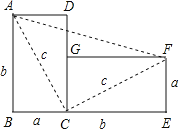
【题目】如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF.通过用不同方法计算梯形ABEF的面积可验证勾股定理,请你写出验证的过程.
参考答案:
【答案】a2+b2=c2
【解析】
试题分析:根据S梯形ABEF=S△ABC+S△CEF+S△ACF,利用三角形以及梯形的面积公式即可证明.
证明:∵S梯形ABEF=![]() (EF+AB)BE=
(EF+AB)BE=![]() (a+b)(a+b)=
(a+b)(a+b)=![]() (a+b)2,
(a+b)2,
∵Rt△CDA≌Rt△CGF,
∴∠ACD=∠CFG,
∵∠CFG+∠GCF=90°,
∴∠ACD+∠GCF=90°,
即∠ACF=90°,
∵S梯形ABEF=S△ABC+S△CEF+S△ACF,
∴S梯形ABEF=![]() ab+
ab+![]() ab+
ab+![]() c2,
c2,
∴![]() (a+b)2=
(a+b)2=![]() ab+
ab+![]() ab+
ab+![]() c2
c2
∴a2+2ab+b2=2ab+c2,
∴a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若y=(m-2)x+(m2-4)是正比例函数,则m的取值是( )
A.2 B.-2 C.±2 D.任意实数
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一组数据x1,x2,…,xn的平均数是a,方差是b,则4x1﹣3,4x2﹣3,…,4xn﹣3的平均数是__________,方差是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了迎接春节,某县准备用灯笼美化滨河路,许采用A、B两种不同造型的灯笼共600个.且A型灯笼的数量比B型灯笼的
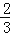 多15个.
多15个. (1)求A、B两种灯笼各需多少个?
(2)已知A、B型灯笼的单价分别为40元、30元,则这次美化工程需多少费用?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
 的图象相交于A(2,3),B(﹣3,n)两点.
的图象相交于A(2,3),B(﹣3,n)两点.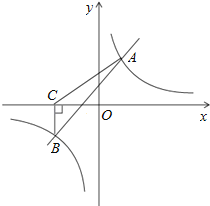
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b>
 的解集;
的解集;(3)过点B作BC⊥x轴,垂足为C,求S△ABC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小区规划在一个长80m,宽40m的长方形草坪上修建三条同样宽的甬道,使其中两条与AB平行,另一条与BC平行,场地的其余部分种草,甬道的宽度为am.

(1)用含x的代数式表示草坪的总面积S;
(2)如果每一块草坪的面积都相等,且甬道的宽为1m,那么每块草坪的面积是多少平方米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】有2012个数排成一行,其中任意相邻的三个数中,中间的数等于它前后两数的和,若第一个数和第二个数都是1,则这2012个数的和等于 ( )
A.-1 B. 0 C. 2 D. 2010
相关试题

