【题目】已知二次函数y=2x2﹣4x﹣6.
(1)写出抛物线的开口方向,对称轴和顶点坐标.
(2)在平面直角坐标系中,画出这个二次函数的图象; 
(3)当x取何值时,y随x的增大而减少?
(4)求函数图象与两坐标轴交点所围成的三角形的面积.
参考答案:
【答案】
(1)解:∵a=2>0,
∴抛物线的开口向上,
∵y=2x2﹣4x﹣6=2(x﹣1)2﹣8,
∴抛物线对称轴为直线x=1,
顶点坐标为(1,﹣8)
(2)解:令y=0,2x2﹣4x﹣6=0,
解得x1=﹣1,x2=3,
所以,抛物线与x轴的交点坐标为(﹣1,0),(3,0),
令x=0,则y=﹣6,
所以,抛物线与y轴的交点坐标为(0,﹣6),
作出函数图象如图所示

(3)解:x<1时,y随x的增大而减少
(4)解:函数图象与x轴的交点设为A、B,则AB=3﹣(﹣1)=3+1=4,
设与y轴的交点坐标为(0,﹣6),则OC=6,
所以,函数图象与两坐标轴交点所围成的三角形的面积= ![]() ABOC=
ABOC= ![]() ×4×6=12
×4×6=12
【解析】(1)根据二次项系数大于0判断出开口向上,将二次函数解析式整理成顶点式形式,然后写成对称轴和顶点坐标即可;(2)求出二次函数与坐标轴的交点,然后作出函数图象即可;(3)根据函数图象与二次函数的增减性解答;(4)利用三角形的面积公式列式计算即可得解.
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一抛物线与x轴的交点是A(﹣2,0)、B(1,0),且经过点C(2,8).
(1)求该抛物线的解析式;
(2)求该抛物线的顶点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点B、E、C、F在一条直线上,AB=DF,AC=DE,∠A=∠D.
(1)求证:AC∥DE;
(2)若BF=13,EC=5,求BC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形
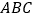 底边
底边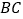 的长为
的长为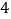 ,面积是
,面积是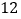 ,腰
,腰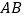 的垂直平分线
的垂直平分线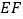 分别交
分别交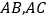 于点
于点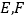 ,若
,若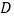 为底边
为底边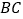 边上的中点,点
边上的中点,点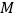 为线段
为线段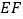 上一动点,则
上一动点,则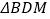 的周长最小值是多少?
的周长最小值是多少?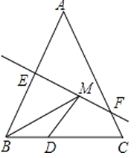
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=12cm,且
 ,BC=10cm,点D为AB的中点.如果点P在线段BC上以2cm/s的速度由点B向C点运动,同时,点Q在线段AC上由点A向C点以4cm/s的速度运动.
,BC=10cm,点D为AB的中点.如果点P在线段BC上以2cm/s的速度由点B向C点运动,同时,点Q在线段AC上由点A向C点以4cm/s的速度运动.(1)若点P、Q两点分别从B、A两点同时出发,经过2秒后,△BPD与△CQP是否全等,请说明理由;
(2)若点P、Q两点分别从B、A两点同时出发,△CPQ的周长为18cm,问:经过几秒后,△CPQ是等腰三角形?

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,既是轴对称图形又是中心对称图形的是( )
A.
等边三角形
B.
平行四边形
C.
正方形
D.
正五边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD,BC于点E,F,下面的结论:
①点E和点F,点B和点D是关于中心O对称点;
②直线BD必经过点O;
③四边形DEOC与四边形BFOA的面积必相等;
④△AOE与△COF成中心对称.
其中正确的个数为( )
A.1
B.2
C.3
D.4
相关试题

