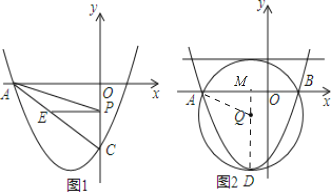
【题目】如图,已知抛物线y=mx2+2mx+c(m≠0),与y轴交于点C(0,﹣4),与x轴交于点A(﹣4,0)和点B.
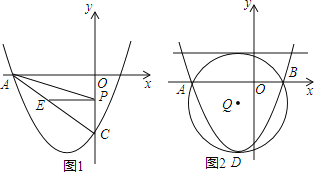
(1)求该抛物线的解析式;
(2)若P是线段OC上的动点,过点P作PE∥OA,交AC于点E,连接AP,当△AEP的面积最大时,求此时点P的坐标;
(3)点D为该抛物线的顶点,⊙Q为△ABD的外接圆,求证⊙Q与直线y=2相切.
参考答案:
【答案】(1)y=![]() x2+x﹣4.(2)P(0,﹣2);(3)见解析
x2+x﹣4.(2)P(0,﹣2);(3)见解析
【解析】
试题分析:审题知:(1)题中已知抛物线上的两个点,只需将点坐标代入抛物线解析式即可求解;
(2)此题只需设出点P的坐标(0,t),并根据题中关系,列出△AEP面积关于t的二次函数即可求解;
(3)此题应先求出圆心Q的坐标,在求出半径,证明圆心到直线的距离等于半径即可.
解:(1)把点C(0,﹣4),点A(﹣4,0)坐标代入:y=mx2+2mx+c(m≠0)得:![]() ,
,
解得: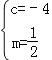 .
.
所以:抛物线的解析式为:y=![]() x2+x﹣4.
x2+x﹣4.
(2)设点P(0,t)﹣4≤t≤0,则有:PC=t+4,OP=﹣t,OA=4
由PE∥OA可知:三角形CPE,三角形POA,三角形AOC均为直角三角形,
所以:![]() ,
,![]() ,解得:PE=t+4
,解得:PE=t+4
所以:S△AEP=![]() ×OA×OC﹣
×OA×OC﹣![]() ×OA×OP﹣
×OA×OP﹣![]() ×PC×PE
×PC×PE
=![]() ×4×4﹣
×4×4﹣![]() ×4×(﹣t)﹣
×4×(﹣t)﹣![]() ×(t+4)×(t+4)
×(t+4)×(t+4)
=﹣![]() t2﹣2t.
t2﹣2t.
所以:当t=﹣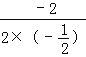 =﹣2时,△AEP的面积最大,
=﹣2时,△AEP的面积最大,
此时:P(0,﹣2);
(3)过点D作DM⊥x轴,垂足为M,
抛物线的解析式为:y=![]() x2+x﹣4=
x2+x﹣4=![]() (x+1)2﹣
(x+1)2﹣![]()
所以:顶点D(﹣1,![]() ),点M(﹣1,0),AM=﹣1﹣(﹣4)=3
),点M(﹣1,0),AM=﹣1﹣(﹣4)=3
由圆和抛物线的对称性可知:圆心Q在DM上,QM⊥AB,
设圆Q的半径为r,则AQ=r,QM=![]() ﹣r,由勾股定理得:
﹣r,由勾股定理得:
r2=![]() +32,解得:r=
+32,解得:r=![]() ,QM=
,QM=![]() ﹣r=
﹣r=![]() ,所以点Q(﹣1,﹣
,所以点Q(﹣1,﹣![]() )
)
因为直线y=2与x轴平行,所以点Q到直线y=2的距离为:2﹣(﹣![]() )=
)=![]() ,
,
所以:圆心Q到直线y=2的距离=圆的半径
所以:⊙Q与直线y=2相切.
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“等腰三角形的两腰上的高线相等” 的逆命题是:_______________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
(1)∠AOD的余角是 ______ ,∠COD的余角是 ______
(2)OE是∠BOC的平分线吗?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣x+b与反比例函数
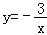 的图象相交于点A(a,3),且与x轴相交于点B.
的图象相交于点A(a,3),且与x轴相交于点B.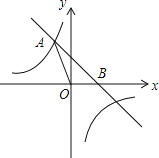
(1)求a、b的值;
(2)若点P在x轴上,且△AOP的面积是△AOB的面积的
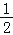 ,求点P的坐标.
,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算并观察下列各式:
(x-1)(x+1)= ______ ;
(x-1)(x2+x+1)= ______ ;
(x-1)(x3+x2+x+1)= ______ ;
(2)从上面的算式及计算结果,你发现了什么?请根据你发现的规律直接写下面的空格.
(x-1)( ______ )=x6-1;
(3)利用你发现的规律计算:
(x-1)(x6+x5+x4+x3+x2+x+1)= _____ ;
(4)利用该规律计算1+4+42+43+…+42013= ______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在-3,-1,1,3四个数中,比-2小的数是( )
A.-3 B.-1 C.1 D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:ax2﹣ax= .
相关试题

