【题目】如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,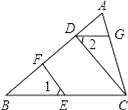
(1)试判断DG与BC的位置关系,并说明理由.
(2)若∠A=70°,∠B=40°,求∠AGD的度数.
参考答案:
【答案】
(1)
解:DG∥BC,
理由是:∵CD⊥AB,EF⊥AB,
∴∠CDB=∠EFB=90°,
∴CD∥EF,
∴∠1=∠BCD,
∵∠1=∠2,
∴∠2=∠BCD,
∴DG∥BC
(2)
解:∵∠A=70°,∠B=40°,
∴∠ACB=180°﹣∠B﹣∠A=70°,
∵DG∥BC,
∴∠AGD=∠ACB=70°
【解析】(1)根据平行线的判定推出CD∥EF,根据平行线的性质得出∠1=∠BCD,求出∠2=∠BCD,根据平行线的判定得出即可;(2)根据三角形内角和定理求出∠ACB,根据平行线的性质得出∠AGD=∠ACB,即可得出答案.
【考点精析】本题主要考查了平行线的判定和平行线的判定与性质的相关知识点,需要掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PA,PB,AB,已知∠PBA=∠C.

(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为
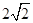 ,求BC的长.
,求BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】﹣2的相反数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣x2﹣2x+2上的三点,则y1,y2,y3的大小关系为( )
A. y1>y2>y3B. y1>y3>y2C. y3>y2>y1D. y3>y1>y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形
 ,图中阴影部分的面积为( )
,图中阴影部分的面积为( )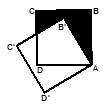
A.
B.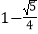
.
C.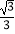
D.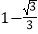
-
科目: 来源: 题型:
查看答案和解析>>【题目】在-1,0,-3,5这四个数中,最小的数是( )
A. -1 B. 0 C. -3 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9
(1)甲队成绩的中位数是分,乙队成绩的众数是分;
(2)计算甲队的平均成绩和方差;
(3)已知乙队成绩的方差是1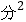 ,则成绩较为整齐的是哪一队.
,则成绩较为整齐的是哪一队.
相关试题

