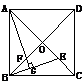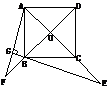3 如图,有一张面积为1的正方形纸片 ,
,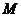 ,
, 分别是
分别是 ,
, 边的中点,将
边的中点,将 点折叠至
点折叠至 上,落在
上,落在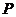 点的位置,折痕为
点的位置,折痕为 ,连结
,连结 ,则
,则 .
.
 4
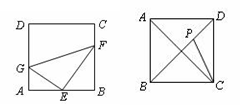
在正方形ABCD中,E为AB边的中点,G,F分别为AD,BC边上的点,若
4
在正方形ABCD中,E为AB边的中点,G,F分别为AD,BC边上的点,若 ,
, ,
, ,则GF的长为 .
,则GF的长为 .
5 如图,已知P是正方形ABCD对角线BD上一点,且BP = BC,
则∠ACP度数是 .
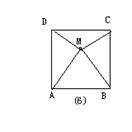
6如图6,在正方形ABCD内取一点M,使△MAB是等边三角形,
那么∠ADM的度数是
三 解下列各题
、1 如图所示,正方形ABCD中,P是对角线AC上一点,PE⊥AB于E,PF⊥BC于F。请猜想EF与PD的数量关系、位置关系,并说明理由。
 2 在以ΔABC的AB、AC为边向外作正方形ABDE及ACGF,作AN⊥BC于点N,延长NA交EF于M点,求证:EM=ME。
2 在以ΔABC的AB、AC为边向外作正方形ABDE及ACGF,作AN⊥BC于点N,延长NA交EF于M点,求证:EM=ME。
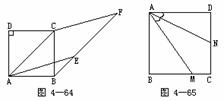
3 如图,在正方形ABCD中,取AD、CD边的中点E、F,连接CE、BF交于点G,连接AG。试判断AG与AB是否相等,并说明道理。
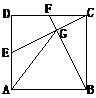
4 如图4-64,已知四边形ABCD是正方形,四边形AEFC是菱形,求∠EAB.
5.已知:如图4-65,正方形ABCD中,M为BC上任一点,AN是∠DAM的平分线,交DC于N点.求证:DN+BM=AM.
6.已知:如图4-66,正方形ABCD中,M为BC上任意一点,N是CD的中点,且AM=DC+CM.求证:AN平分∠DAM.
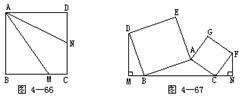 7.已知:如图4-67,正方形ABDE和正方形ACFG中,DM⊥BC,FN⊥BC.求证:BC=DM+FN.
7.已知:如图4-67,正方形ABDE和正方形ACFG中,DM⊥BC,FN⊥BC.求证:BC=DM+FN.
8 已知:如图4-80,正方形ABCD中,M是BC上一点,MN⊥AM,MN交∠DCE平分线于N,E在BC延长线上.求证:AM=MN.
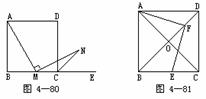 9.已知:如图4-81,正方形ABCD中,AC,BD相交于O,E,F分别为BC,OD中点.求证:AF⊥EF.
9.已知:如图4-81,正方形ABCD中,AC,BD相交于O,E,F分别为BC,OD中点.求证:AF⊥EF.
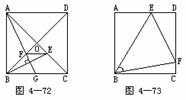
10 已知:如图4-72,正方形ABCD的对角线BD,AC相交于O,E为OC上任一点,连结BE,作AG⊥BE,交BD于F,交BC于G.求证:EF∥BC.
11.已知:如图4-73,正方形ABCD中,∠EBF=45°,E,F分别在AD和DC上.求证:EF=AE+FC.
 |
12 如图,正方形ABCD中对角线AC、BD相交于O,E为AC上一点,AG⊥EB交EB于G,AG交BD于F。
(1) 说明OE=OF的道理;
(2) 在(1)中,若E为AC延长线上,AG⊥EB交EB的延长线于G,AG、BD的延长线交于F,其他条件不变,如图2,则结论:“OE=OF”还成立吗?请说明理由。
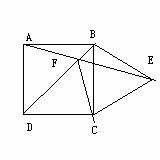 13 以正方形ABCD的一边BC向形外作等边三角形BCE,连接AE、BD交于F,连接FC。
13 以正方形ABCD的一边BC向形外作等边三角形BCE,连接AE、BD交于F,连接FC。
求∠BCF的度数