解:取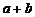 与取
与取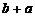 是同一种取法.分类标准为两加数的奇偶性,第一类,偶偶相加,由分步计数原理得(10×9)/2=45种取法,第二类,奇奇相加,也有(10×9)/2=45种取法.根据分类计数原理共有45+45=90种不同取法.
是同一种取法.分类标准为两加数的奇偶性,第一类,偶偶相加,由分步计数原理得(10×9)/2=45种取法,第二类,奇奇相加,也有(10×9)/2=45种取法.根据分类计数原理共有45+45=90种不同取法.
例2 在1~20共20个整数中取两个数相加,使其和大于20的不同取法共有多少种?
解:分类标准一,固定小加数.小加数为1时,大加数只有20这1种取法;小加数为2时,大加数有19或20两种取法;小加数为3时,大加数为18,19或20共3种取法…小加数为10时,大加数为11,12,…,20共10种取法;小加数为11时,大加数有9种取法…小加数取19时,大加数有1种取法.由分类计数原理,得不同取法共有1+2+…+9+10+9+…+2+1=100种.
分类标准二:固定和的值.有和为21,22,…,39这几类,依次有取法10,9,9,8,8, …,2,2,1,1种.由分类计数原理得不同取法共有10+9+9+…+2+2+1+1=100种.
例3 如图一,要给①,②,③,④四块区域分别涂上五种颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同颜色,则不同涂色方法种数为()
A.
180 B. 
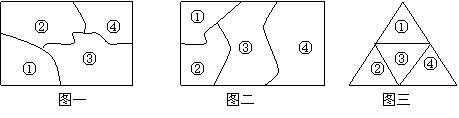
若变为图二,图三呢?(240种,5×4×4×4=320种)
例4 如下图,共有多少个不同的三角形?
解:所有不同的三角形可分为三类”
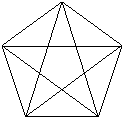 第一类:其中有两条边是原五边形的边,这样的三角形共有5个
第一类:其中有两条边是原五边形的边,这样的三角形共有5个
第二类:其中有且只有一条边是原五边形的边,这样的三角形共有5×4=20个
第三类:没有一条边是原五边形的边,即由五条对角线围成的三角形,共有5+5=10个
由分类计数原理得,不同的三角形共有5+20+10=35个.
例5 75600有多少个正约数?有多少个奇约数?
解:75600的约数就是能整除75600的整数,所以本题就是分别求能整除75600的整数和奇约数的个数.
由于 75600=24×33×52×7
(1) 75600的每个约数都可以写成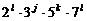 的形式,其中
的形式,其中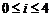 ,
,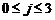 ,
,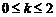 ,
,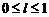
于是,要确定75600的一个约数,可分四步完成,即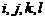 分别在各自的范围内任取一个值,这样
分别在各自的范围内任取一个值,这样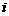 有5种取法,
有5种取法,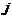 有4种取法,
有4种取法,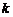 有3种取法,
有3种取法,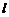 有2种取法,根据分步计数原理得约数的个数为5×4×3×2=120个.
有2种取法,根据分步计数原理得约数的个数为5×4×3×2=120个.
(2)奇约数中步不含有2的因数,因此75600的每个奇约数都可以写成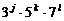 的形式,同上奇约数的个数为4×3×2=24个.
的形式,同上奇约数的个数为4×3×2=24个.
1.用1,2,3,4,5可组成多少个三位数?(各位上的数字允许重复)
2.用数字1,2,3可写出多少个小于1000的正整数? (各位上的数字允许重复)
3.集合A={a,b,c,d,e},集合B={1,2,3},问A到B的不同映射f共有多少个?B到A的映射g共有多少个?
4.将3封信投入4个不同的邮筒的投法共有多少种?
5. 4名学生从3个不同的楼梯下楼的方法数.
6. 4名学生分配到3个车间去劳动,共有多少中不同的分配方案?
7. 求集合{1,2,3,4,5}的子集的个数
答案:1. 5×5×5×5=625 2. 3+32+33=39 3. 35,53 4. 43 5. 34 6. 34
7. 在集合{1,2,3,4,5}的子集中,每个元素都只有出现和不出现这2种可能,所以这个集合的子集的个数为2×2×2×2×2=25=32个.
五、课后作业: 
1.用0,1,2,3,4,5这六个数字,
(1)可以组成多少个数字不重复的三位数?
(2)可以组成多少个数字允许重复的三位数?
(3)可以组成多少个数字不允许重复的三位数的奇数?
(4)可以组成多少个数字不重复的小于1000的自然数?
(5)可以组成多少个大于3000,小于5421的数字不重复的四位数?
解(1)分三步:①先选百位数字.由于0不能作百位数,因此有5种选法;②十位数字有5种选法;
③个位数字有4种选法.由乘法原理知所求不同三位数共有5×5×4=100个.
(2)分三步:(1)百位数字有5种选法;(ii)十位数字有6位选法;(iii)个位数字有6种选法.
所求三位数共有5×6×6=180个.
(3)分三步:①先选个位数字,有3种选法;②再选百位数字,有4种选法;③选十位数字也是4
种选法,所求三位奇数共有3×4×4=48个.
(4)分三类:①一位数,共有6个;②两位数,共有5×5=25个;③三位数共有5×5×4=100个.
因此,比1000小的自然数共有6+25+100=131个.
(5)分4类:①千位数字为3,4之一时,共有2×5×4×3=120个;②千位数字为5,百位数字为
0,1,2,3之一时,共有4×4×3=48个;③千位数字是5,百位数字是4,十位数字为0,1之一
时,共有2×3=6个;④还有5420也是满条件的1个.故所求自然数共120+48+6+1=175个.
说明:⑴排数字问题是最常见的一种类型,要特别注意首位不能排0.
⑵第(5)题改成:可以组成多少个大于3000,小于5421的四位数?
答案:2*6*6*6+4*6*6+2*6+1=589个
2.求下列集合的元素个数.
(1)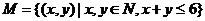 ;
;
(2)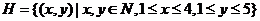 .
.
解:(1)分7类:①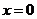 ,
,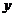 有7种取法;②
有7种取法;②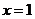 ,
,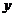 有6种取法; ③
有6种取法; ③ ,
,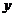 有5种取法; ④
有5种取法; ④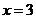 ,
,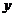 有4种取法; ⑤
有4种取法; ⑤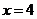 ,
,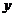 有3种取法; ⑥
有3种取法; ⑥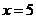 ,
,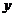 有2种取法;⑦
有2种取法;⑦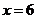 ,
,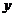 只有1种取法
只有1种取法 因此
因此 共有
共有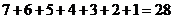 个元素
个元素
(2)分两步:①先选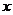 ,有4种可能;②再选
,有4种可能;②再选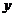 有5种可能.由乘法原理,
有5种可能.由乘法原理,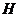 共有
共有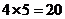 个元素
个元素
3.有四位同学参加三项不同的比赛,
(1)每位同学必须参加一项竞赛,有多少种不同的结果?
(2)每项竞赛只许一位学生参加,有多少种不同的结果?
解:(1)每位学生有三种选择,四位学生共有参赛方法: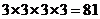 种;
种;
(2)每项竞赛被选择的方法有四种,三项竞赛共有参赛方法: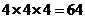 种.
种.
4.①设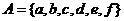 ,
,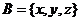 ,从
,从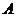 到
到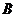 共有多少个不同映射?
共有多少个不同映射?
②6个人分到3个车间,共有多少种分法?
解:(1)分6步:先选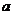 的象,有3种可能,再选
的象,有3种可能,再选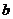 的象也是3种可能,…,选
的象也是3种可能,…,选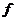 象也有3种可能, 由乘法原理知,共有
象也有3种可能, 由乘法原理知,共有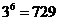 种不同映射;
种不同映射;
(2)把6个人构成的集合,看成上面(1)中之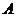 ,3个车间构成的集合,看成上面的
,3个车间构成的集合,看成上面的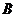 , 因此,所求问题转化为映射问题,如上题所述,共有
, 因此,所求问题转化为映射问题,如上题所述,共有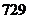 种方案
种方案
5.甲、乙、丙、丁四个人各写一张贺卡,放在一起,再各取一张不是自己所写的贺卡,共有多少种不同的取法?
解:列表排出所有的分配方案,共有3+3+3=9种,或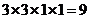 种.
种.
六、板书设计(略) 
七、课后记: 

