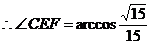(4)(2009年4月北京海淀区高三一模文)已知 是直线,
是直线,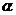 、
、 是两个不同平面,下列命题中真命题是( C )
是两个不同平面,下列命题中真命题是( C )
(A)若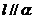 ,
,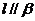 ,则
,则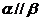 (B)若
(B)若 ,
,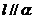 ,则
,则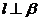
(C)若 ,
,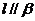 ,则
,则 (D)若
(D)若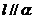 ,
,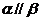 ,则
,则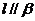
4.(北京市石景山区2009年4月高三一模理)对于两条直线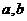 和平面
和平面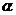 ,若
,若 ,则“
,则“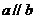 ”是“
”是“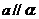 ”的(D)
”的(D)
A.充分但不必要条件
B.必要但不充分条件
C.充要条件
D.既不充分也不必要条件
(5) (北京市朝阳区2009年4月高三一模理)用一平面去截体积为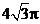 的球,所得截面的面积为
的球,所得截面的面积为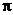 ,则球心到截面的距离为( C )
,则球心到截面的距离为( C )
A. 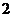 B.
B.
 C.
C.
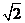 D.
D.
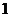
5. (北京市西城区2009年4月高三一模抽样测试文理)已知直线a 和平面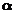 ,那么
,那么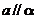 的一个充分条件是( C )
的一个充分条件是( C )

A. 存在一条直线b, B. 存在一条直线b,
B. 存在一条直线b,

C. 存在一个平面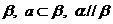 D. 存在一个平面
D. 存在一个平面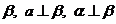
5. (北京市崇文区2009年3月高三统一考试理) 已知m、n是两条不重合的直线,α、β、γ是三个不重合的平面,则α//β的一个充分条件是 ( D )
A.m α,m
α,m β
B.α⊥γ,β⊥γ
β
B.α⊥γ,β⊥γ
C.m⊂α,n⊂β, m∥n D. m、n是异面直线,m⊂α,m∥β,n⊂β,n∥α
5.(北京市崇文区2009年3月高三统一考试文)下列命题中,正确的命题是 ( B )
A.过空间任一点P均存在着与平面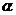 平行的直线
平行的直线
B.过空间任一点P均存在着与平面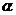 垂直的直线
垂直的直线
C.过空间任一点P均存在着与平面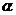 平行的无数多条直线
平行的无数多条直线
D.过空间任一点P均存在着与平面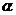 垂直的无数多条直线
垂直的无数多条直线
5.(北京市东城区2009年3月高中示范校高三质量检测文理)两个平面 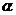 与
与 相交但不垂直,直线
相交但不垂直,直线 在平面
在平面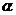 内,则在平面
内,则在平面 内 ( C )
内 ( C )
A.一定存在与直线 平行的直线
B.一定不存在与直线
平行的直线
B.一定不存在与直线 平行的直线
平行的直线
C.一定存在与直线 垂直的直线
D.不一定存在与直线
垂直的直线
D.不一定存在与直线 垂直的直线
垂直的直线
3. (北京市丰台区2009年3月高三统一检测理)已知直线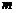
 平面α ,直线
平面α ,直线
 平面α ,“直线c⊥
平面α ,“直线c⊥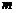 ,直线c⊥
,直线c⊥ ”是“直线c⊥平面α”的
”是“直线c⊥平面α”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充要条件 (D)既不充分也不必要条件
(12)(2009年4月北京海淀区高三一模文)已知四面体 ―
―
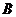
 中,
中, ,且
,且 ,
,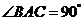 ,则异面直线
,则异面直线 与
与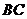 所成的角为
.
所成的角为
. 
12.(北京市石景山区2009年4月高三一模理)设地球半径为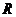 ,在北纬
,在北纬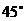 圈上有甲、乙两地,它们的经度差为
圈上有甲、乙两地,它们的经度差为 ,则甲、乙两地间的最短纬线之长为 ,甲、乙两地的球面距离为 .
,则甲、乙两地间的最短纬线之长为 ,甲、乙两地的球面距离为 .
答案: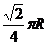 ,
,
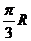
13. (北京市西城区2009年4月高三一模抽样测试文)已知一个正方体的八个顶点都在同一个球面上. 设此正方体的表面积为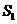 ,球的表面积
,球的表面积 ,则
,则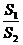 =_____________.
=_____________.
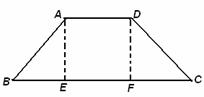 11. (北京市崇文区2009年3月高三统一考试理)如图,等腰梯形ABCD中, E,F分别是BC 上三等分点,AD=AE=1,BC=3,
,若把三角形ABE和DCF分别沿AE和DF折起,使得B、C两点重合于一点P,则二面角P-AD-E的大小为
.
11. (北京市崇文区2009年3月高三统一考试理)如图,等腰梯形ABCD中, E,F分别是BC 上三等分点,AD=AE=1,BC=3,
,若把三角形ABE和DCF分别沿AE和DF折起,使得B、C两点重合于一点P,则二面角P-AD-E的大小为
. 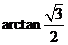
 12. (北京市崇文区2009年3月高三统一考试文)如图,等腰梯形ABCD中, E,F分别是BC边上的三等分点,AD=AE=1,BC=3,
,若把三角形ABE和DCF分别沿AE和DF折起,使得B、C两点重合于一点P,则二面角P-EF-D的大小为 .
12. (北京市崇文区2009年3月高三统一考试文)如图,等腰梯形ABCD中, E,F分别是BC边上的三等分点,AD=AE=1,BC=3,
,若把三角形ABE和DCF分别沿AE和DF折起,使得B、C两点重合于一点P,则二面角P-EF-D的大小为 . 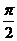
11. (北京市丰台区2009年3月高三统一检测理)在长方体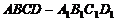 中,
中, ,若点
,若点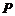 到
到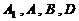 这四点的距离相等,则
这四点的距离相等,则 =
。
=
。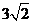
12. (北京市丰台区2009年3月高三统一检测文) 在长方体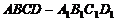 中,
中, ,则长方体的对角线长为 。
,则长方体的对角线长为 。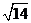
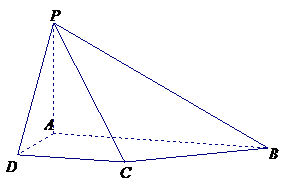 (16)(2009年4月北京海淀区高三一模文)(本小题共14分)如图,四棱锥
(16)(2009年4月北京海淀区高三一模文)(本小题共14分)如图,四棱锥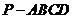 中,
中, 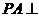 平面
平面 ,底面
,底面 为直角梯形,且
为直角梯形,且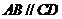 ,
, ,
, ,
,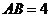 .
.
(I)求证: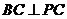 ;
;
(II)求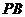 与平面
与平面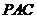 所成的角的正弦值;
所成的角的正弦值;
(III)求点 到平面
到平面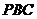 的距离.
的距离.
16解:方法1
(I)证明:在直角梯形 中,
中,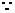
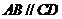 ,
, ,
,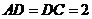
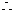
 ,且
,且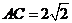 .
………………………1分
.
………………………1分
取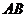 的中点
的中点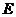 ,连结
,连结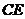 ,
,
由题意可知,四边形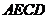 为正方形,所以
为正方形,所以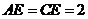 ,
,
又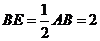 ,所以
,所以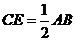 ,
,
则 为等腰直角三角形,
为等腰直角三角形,
所以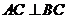 ,
………………………2分
,
………………………2分
又因为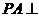 平面
平面 ,且
,且 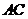 为
为 在平面
在平面 内的射影,
内的射影, 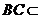 平面
平面 ,由三垂线定理得,
,由三垂线定理得,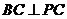 ………………………4分
………………………4分
(II)由(I)可知,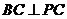 ,
,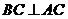 ,
,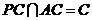 ,
,
所以 平面
平面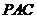 ,………………5分
,………………5分
 是
是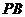 在平面
在平面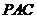 内的射影,所以
内的射影,所以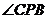 是
是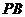 与平面
与平面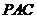 所成的角,……6分
所成的角,……6分
又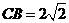 ,………………7分
,………………7分
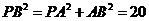 ,
, ,………………8分
,………………8分
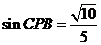 ,即
,即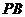 与平面
与平面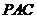 所成角的正弦为
所成角的正弦为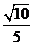 …………9分
…………9分
(III)由(II)可知, 平面
平面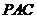 ,
,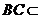 平面
平面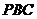 ,
,
所以平面 平面
平面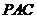 ,
………………10分
,
………………10分
过 点在平面
点在平面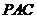 内作
内作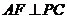 于
于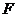 ,所以
,所以 平面
平面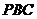 ,
,
则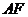 的长即为点
的长即为点 到平面
到平面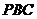 的距离,
………………11分
的距离,
………………11分
在直角三角形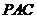 中,
中,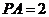 ,
,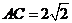 , ………………12分
, ………………12分
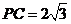 ,
……………13分
,
……………13分
所以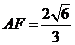 即点
即点 到平面
到平面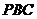 的距离为
的距离为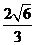 …………14分
…………14分
方法2
∵ 平面
平面 ,
,
∴以A为原点,AD、AB、AP分别为x、y、z轴,建立空间直角坐标系…………1分
∵ ,
,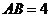 .
.
∴ B (0,4,0), D (2,0 ,0) , C (2,2,0) , P ( 0,0,2) …………2分
(I)∴
∵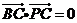 ………………3分
………………3分
∴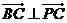 , 即
, 即 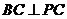 ………………4分
………………4分
(II) ∵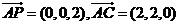 设面APC法向量
设面APC法向量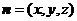
∴ ∴
∴ ………………6分
………………6分
设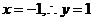 ∴
∴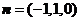 ………………7分
………………7分
∵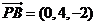 ∴
∴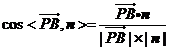 ………8分
………8分
=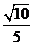 ………………9分
………………9分
即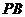 与平面
与平面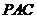 所成角的正弦值为
所成角的正弦值为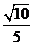
(III)由∵ 设面
设面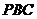 法向量
法向量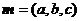
∴ ∴
∴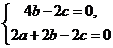 ………………11分
………………11分
设 ∴
∴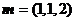 ………………12分
………………12分
∴点 到平面
到平面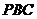 的距离为
的距离为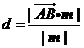 ………………13分
………………13分
=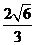
∴点 到平面
到平面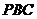 的距离为
的距离为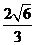 ………………14分
………………14分
17.(北京市石景山区2009年4月高三一模理)(本题满分14分)
 如图,已知正三棱柱
如图,已知正三棱柱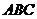 ―
―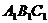 的底面边长是
的底面边长是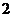 ,
,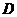 是侧棱
是侧棱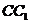 的中点,直线
的中点,直线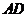 与侧面
与侧面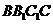 所成的角为
所成的角为 .
.
(Ⅰ)求此正三棱柱的侧棱长;
(Ⅱ)求二面角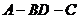 的大小;
的大小;
(Ⅲ)求点 到平面
到平面 的距离.
的距离.
17.(本题满分 分)
分)
解法一:
(Ⅰ)设正三棱柱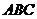 ―
―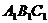 的侧棱长为
的侧棱长为 .取
.取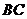 中点
中点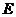 ,连结
,连结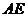 .
.
 ∵
∵
 是正三角形,∴
是正三角形,∴ 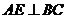 .
.
又底面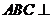 侧面
侧面 ,
,
且两平面交线为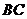 ,
,
∴
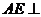 侧面
侧面 .
.
连结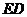 ,则
,则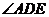 为直线
为直线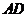 与侧面
与侧面 所成的角.
所成的角.
∴
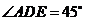 .
………………2分
.
………………2分
在 中,
中,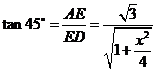 ,解得
,解得 .
.
∴
此正三棱柱的侧棱长为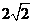 .
………………4分
.
………………4分
(Ⅱ)过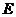 作
作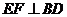 于
于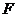 ,连结
,连结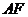 .
.
∵
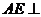 侧面
侧面 ,∴
,∴  是
是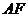 在平面
在平面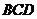 内的射影.
内的射影.
由三垂线定理,可知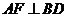 .
.
∴ 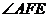 为二面角
为二面角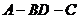 的平面角.
………………6分
的平面角.
………………6分
在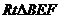 中,
中, ,又
,又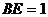 ,
,
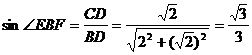 , ∴
, ∴
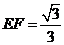 .
.
又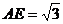 ,
,
∴
在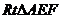 中,
中,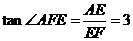 .
………………8分
.
………………8分
故二面角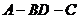 的大小为
的大小为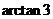 .
………………9分
.
………………9分
(Ⅲ)由(Ⅱ)可知,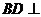 平面
平面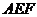 ,
,
∴
平面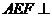 平面
平面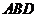 ,且交线为
,且交线为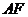 ,
,
过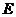 作
作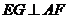 于
于 ,则
,则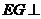 平面
平面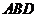 .
.
∴
 的长为点
的长为点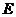 到平面
到平面 的距离.
………………10分
的距离.
………………10分
在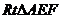 中,
中,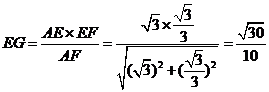 . …………12分
. …………12分
∵
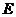 为
为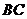 中点,∴ 点
中点,∴ 点 到平面
到平面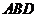 的距离为
的距离为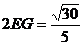 . …………14分
. …………14分
解法二:
(Ⅰ)同解法一.
(Ⅱ)如图,建立空间直角坐标系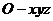 .
.
则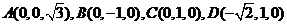 .
.
设
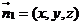 为平面
为平面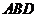 的法向量.
的法向量.
 由
由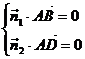 ,
,
得 .
.
取 .
…………6分
.
…………6分
又平面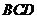 的一个法向量
的一个法向量 .
…………7分
.
…………7分
∴
 . …………8分
. …………8分
结合图形可知,二面角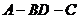 的大小为
的大小为 .
…………9分
.
…………9分
(Ⅲ)由(Ⅱ), ,
,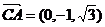 .
…………10分
.
…………10分
∴
点 到平面
到平面 的距离
的距离

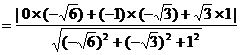
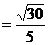 .
.
∴ 点 到平面
到平面 的距离为
的距离为 .
…………14分
.
…………14分
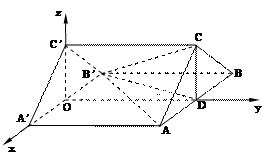
(17) (北京市朝阳区2009年4月高三一模) (本小题满分14分)
 如图,在直三棱柱
如图,在直三棱柱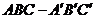 中, 已知
中, 已知 ,
,  ,
,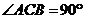 ,
,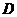 是
是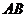 的中点.
的中点.
(Ⅰ)求证: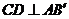 ;
;
(Ⅱ)求二面角 的大小;
的大小;
(理)(Ⅲ)求直线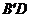 与平面
与平面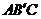 所成角的正弦值.
所成角的正弦值.
(17) 解法一:
(Ⅰ)证明:因为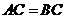 ,
,

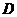 是
是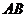 的中点,所以
的中点,所以 .
.
由已知,三棱柱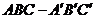 是直三棱柱,
是直三棱柱,
所以平面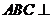 平面
平面 .
.
所以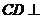 平面
平面 .
.
又因为 平面
平面 ,
,
所以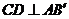 .
………………5分
.
………………5分
(Ⅱ)解:由(1)知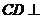 平面
平面 .
.
过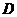 作
作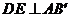 ,垂足为
,垂足为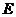 ,连结
,连结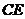 .
.
由三垂线定理可知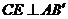 ,
,
所以 是二面角
是二面角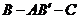 的平面角.
的平面角.
由已知可求得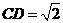 ,
, , 所以
, 所以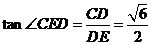 .
.
所以二面角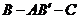 的大小为
的大小为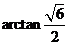 .
.
由于二面角 与二面角
与二面角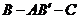 的大小互补,
的大小互补,
所以二面角 的大小为
的大小为 .
………………10分
.
………………10分
(理)(Ⅲ)过D作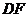
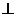
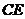 ,垂足为
,垂足为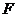 ,连结
,连结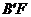 .
.
由(Ⅱ)可证得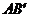
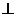 平面
平面 ,所以
,所以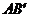
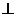
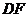 ,可证得
,可证得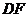
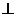 平面
平面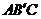 .
.
所以,  为直线
为直线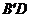 与平面
与平面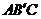 所成的角.
所成的角.
在直角三角形 中,可知
中,可知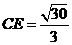 ,所以
,所以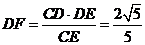 .
.
在直角三角形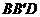 中,可知
中,可知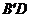 =
=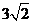 .
.
在直角三角形 中,
中, =
=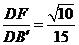 .
.
所以直线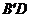 与平面
与平面 所成角的正弦值为
所成角的正弦值为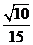 . ………………14分
. ………………14分
解法二:
以 的中点
的中点 为原点,先证明
为原点,先证明 平面
平面 ,建立空间直角坐标系(如图).由已知可得
,建立空间直角坐标系(如图).由已知可得
 、
、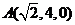 、
、 、
、 、
、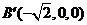 、
、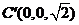 .
.
(Ⅰ)证明: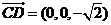 ,
, .
.
因为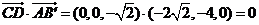 ,
,
所以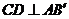 .
………………5分
.
………………5分
(Ⅱ)解: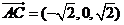 .
.
设平面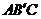 的一个法向量为
的一个法向量为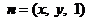 ,
,
由 得
得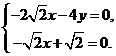
解得 所以
所以 .
.
又知, 平面
平面 ,所以
,所以 为平面
为平面 的法向量.
的法向量.
因为 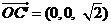 ,所以
,所以 
由图可知,二面角 大于90º,
大于90º,
所以二面角 的大小为
的大小为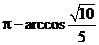 .
………………10分
.
………………10分
(Ⅲ)由(Ⅱ)可知平面 的一个法向量
的一个法向量 ,
,
又 .
.
所以 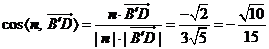 .
.
因为直线 与平面
与平面 所成角为
所成角为 ,
,
所以直线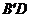 与平面
与平面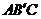 所成角的正弦值为
所成角的正弦值为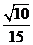 .
………………14分
.
………………14分
17. (北京市西城区2009年4月高三一模抽样测试理)(本小题满分14分)
 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形, 又
又
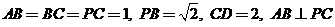 .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求二面角B-PD-C的大小;
(Ⅲ)求点B到平面PAD的距离.
17.(本小题满分14分)
(Ⅰ)证明:在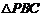 中,
中,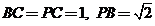 ,
,
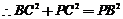 ,
,
 ,即
,即 ,
---------------------------1分
,
---------------------------1分
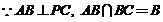 ,
,
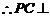 平面
平面 .
---------------------------4分
.
---------------------------4分
(Ⅱ)方法一:
解:由(Ⅰ)知 ,
,
又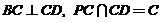 ,
,
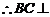 平面
平面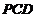 ,
---------------------------5分
,
---------------------------5分
如图,过C作 于M,连接BM,
于M,连接BM,
 是BM在平面PCD内的射影,
是BM在平面PCD内的射影,
 ,
,
又
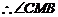 为二面角B-PD-C的平面角.
---------------------------7分
为二面角B-PD-C的平面角.
---------------------------7分
在 中,
中,  ,
PC=1,
,
PC=1,  ,
,

 ,
,
又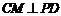 ,
,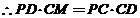 ,
,
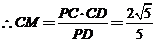 . ---------------8分
. ---------------8分
在 中,
中, 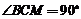 ,
BC=1,
,
BC=1, 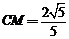 ,
,
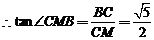 ,
,
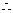 二面角B-PD-C的大小为
二面角B-PD-C的大小为 .
---------------------------9分
.
---------------------------9分
方法二:
 解:如图,在平面ABCD内,以C为原点, CD、CB、CP分别为x、y、z轴,建立空间直角坐标系C-xyz,
解:如图,在平面ABCD内,以C为原点, CD、CB、CP分别为x、y、z轴,建立空间直角坐标系C-xyz,
则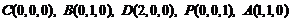 ,
---------------------------5分
,
---------------------------5分
过C作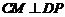 于M,连接BM,设
于M,连接BM,设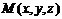 ,
,
则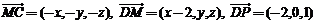 ,
,
 ,
,
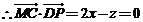 ;
1
;
1
 共线,
共线,
 ,
2
,
2
由12,解得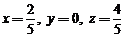 ,
,
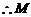 点的坐标为
点的坐标为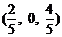 ,
,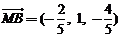 ,
,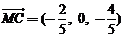 ,
,
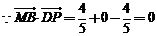 ,
,
 ,
,
又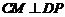 ,
,
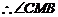 为二面角B-PD-C的平面角.
---------------------------7分
为二面角B-PD-C的平面角.
---------------------------7分
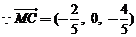 ,
,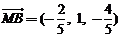 ,
,
 ,
,
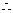 二面角B-PD-C的大小为
二面角B-PD-C的大小为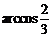 .
--------------------------9分
.
--------------------------9分
(Ⅲ)解:设点B到平面PAD的距离为h,
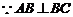 ,
,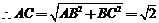 ,
,
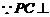 平面ABCD,
平面ABCD,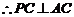 ,
,
 ,
,
在直角梯形ABCD中, ,
,
 .
.
在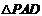 中,
中,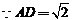 ,
, ,
,
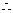
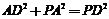 ,
,
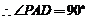 ,
,
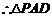 的面积
的面积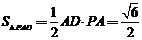 ,
---------------------------10分
,
---------------------------10分
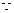 三棱锥B-PAD的体积
三棱锥B-PAD的体积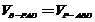 ,
,
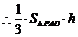
 ,
---------------------------12分
,
---------------------------12分
即 ,解得
,解得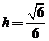 ,
,
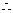 点B到平面PAD的距离为
点B到平面PAD的距离为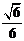 .
---------------------------14分
.
---------------------------14分
17. (北京市西城区2009年4月高三一模抽样测试文)(本小题满分14分)
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形, 又
又
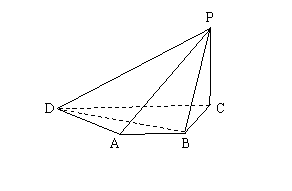
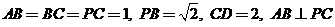 .
.
(Ⅰ) 求证: 平面
平面 ;
;
(Ⅱ) 求PA与平面ABCD所成角的大小;
(Ⅲ) 求二面角B-PD-C的大小.
17.(本小题满分14分)
方法一:(Ⅰ)证明:在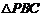 中,
中,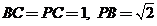 ,
,
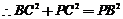 ,
,
 ,即
,即 ,
---------------------------1分
,
---------------------------1分
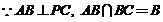 ,
,
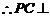 平面
平面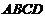 .
---------------------------4分
.
---------------------------4分
 (Ⅱ)如图,连接AC,由(Ⅰ)知
(Ⅱ)如图,连接AC,由(Ⅰ)知 平面
平面 ,
,
 AC为PA在平面ABCD内的射影,
AC为PA在平面ABCD内的射影,
 为PA与平面ABCD所成的角. --------------6分
为PA与平面ABCD所成的角. --------------6分
在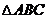 中,
中, ,
, ,
,
 ,
,
在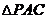 中,
中,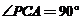 ,
,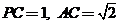 ,
,
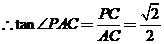 ,
,
 PA与平面ABCD所成角的大小为
PA与平面ABCD所成角的大小为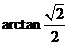 .
---------------------------8分
.
---------------------------8分
(Ⅲ)由(Ⅰ)知 ,
,
又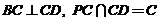 ,
,
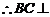 平面
平面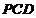 .
---------------------------9分
.
---------------------------9分
如图,过C作 于M,连接BM,
于M,连接BM,
 是BM在平面PCD内的射影,
是BM在平面PCD内的射影,
 ,
,
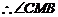 为二面角B-PD-C的平面角.
---------------------------11分
为二面角B-PD-C的平面角.
---------------------------11分
在 中,
中,  ,
PC=1,
,
PC=1,  ,
,
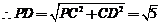 ,
,
又 ,
,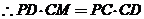 ,
,
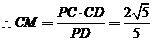 ,
,
在 中,
中, 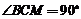 ,
BC=1,
,
BC=1, 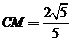 ,
,
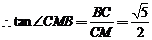 ,
,
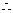 二面角B-PD-C的大小为
二面角B-PD-C的大小为 .
--------------------------14分
.
--------------------------14分
方法二:(Ⅰ)同方法一. ---------------------------4分
(Ⅱ)解:连接AC,由(Ⅰ)知 平面
平面 ,
,
 AC为PA在平面ABCD内的射影,
AC为PA在平面ABCD内的射影,
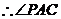 为PA与平面ABCD所成的角.
---------------------------6分
为PA与平面ABCD所成的角.
---------------------------6分
如图,在平面ABCD内,以C为原点, CD、CB、CP分别为x、y、z轴,建立空间直角坐标系C-xyz,
则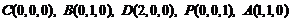 ,
,
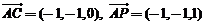 ,
,
---------------------------7分
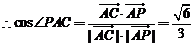 ,
,

 PA与平面ABCD所成角的大小为
PA与平面ABCD所成角的大小为 .
---------------------------9分
.
---------------------------9分
(Ⅲ)过C作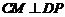 于M,连接BM,设
于M,连接BM,设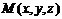 ,
,
则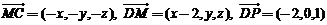 ,
,
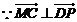 ,
,
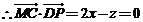 ;
1
;
1
 共线,
共线,
 ,
2
,
2
由12,解得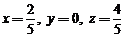 ,
,
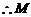 点的坐标为
点的坐标为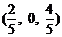 ,
,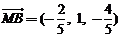 ,
,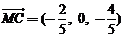 ,
,
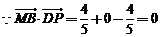 ,
,
 ,
,
又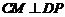 ,
,
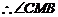 为二面角B-PD-C的平面角.
---------------------------12分
为二面角B-PD-C的平面角.
---------------------------12分
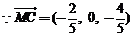 ,
,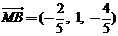 ,
,
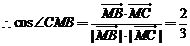 ,
,
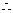 二面角B-PD-C的大小为
二面角B-PD-C的大小为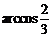 .
--------------------------14分
.
--------------------------14分
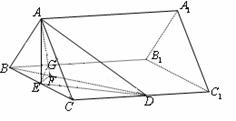
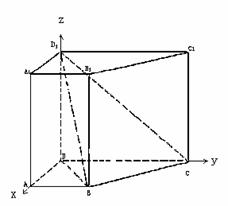
16.(北京市崇文区2009年3月高三统一考试理)(本小题满分14分)
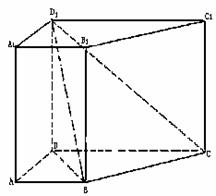 在直四棱柱ABCD-A1B
在直四棱柱ABCD-A1B
(I)求证:BC⊥面D1DB;
(II)求D1B与平面D1DCC1所成角的大小;
(III)在BB1上是否存在一点F,使F到平面D1BC的距离为 ,若存在,则指出该点的位置;若不存在,请说明理由.
,若存在,则指出该点的位置;若不存在,请说明理由.
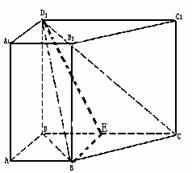
16.(本小题满分14分)
 解法一:
解法一:
(I)证明:∵ABCD-A1B
∴ D1D⊥平面ABCD,
∴BC⊥D1D.
∵AB//CD, AB⊥AD.
∴四边形ABCD为直角梯形,
又∵AB=AD=1,CD=2,
可知BC⊥DB.
∵D1D∩ DB=D,
∴BC⊥平面D1DB. -----------------------4分
(II)取DC中点E,连结BE,D1E.
∵DB=BC,
∴BE⊥CD.
∵ABCD-A1B
∴ABCD⊥D1DCC1.
∴BE⊥D1DCC1.
∴D1E为D1B在平面D1DCC1上的射影,
∴∠BD1E为所求角.
在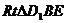 中,
中,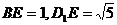 .
.
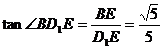 .
.
∴所求角为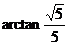 .
---------------------------------9分
.
---------------------------------9分
(Ⅲ)假设B1B存在点F,设BF= x,
∵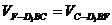 ,BC⊥平面D1BF,
,BC⊥平面D1BF,
∴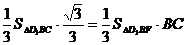 .
.
∵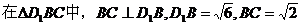 ,
,
∴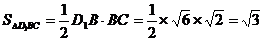 .
.
又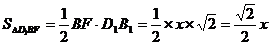 ,
,
∴ .
.
即存在点F为B1B的中点. ---------------14分
 解法二:
解法二:
(I)证明:如图建立坐标系D-xyz,
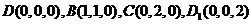 .
.
∴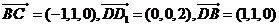 .
.
∵ ,
,
∴BC⊥DD1, BC⊥DB.
∵D1D∩ DB=D,
∴BC⊥平面D1DB. ------------------4分
(II) 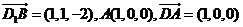 .
.
∵AD⊥平面D1DCC1,
∴平面D1DCC1的法向量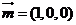 ,
,
∵ .
.
∴D1B与平面D1DCC1所成角的大小为 .
--------------------9分
.
--------------------9分
(III) 假设B1B存在点F,设BF = a,则F(1,1,a),
设平面D1BC的法向量为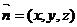 ,
,
由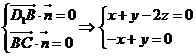 .令x=1,则y = z =1.
.令x=1,则y = z =1.
∴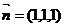 ,又
,又 ,
,
∴ .
.
∵F到平面D1BC的距离为 ,
,
 .
.
即存在点F为B1B的中点. -------------------------------------------14分
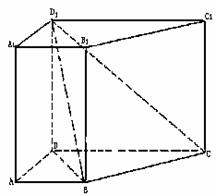 16.(北京市崇文区2009年3月高三统一考试文)(本小题满分14分)
16.(北京市崇文区2009年3月高三统一考试文)(本小题满分14分)
已知直四棱柱ABCD-A1B
(I)求证:BC⊥面D1DB;
(II)求D1B与平面D1DCC1所成角的大小.
16.(本小题满分14分)
解法一:
(I)证明:∵ABCD-A1B
∴ D1D⊥平面ABCD,
∴BC⊥D1D.
∵AB//CD, AB⊥AD.
∴四边形 ABCD为直角梯形,
又∵AB=AD=1,CD=2,
可知BC⊥DB.
∵D1D∩ DB=D,
∴BC⊥平面D1DB. -----------------------6分
(II)取DC中点E,连结BE,D1E.
∵DB=BC,
∴BE⊥CD.
∵ABCD-A1B
∴ABCD⊥D1DCC1.
∴BE⊥D1DCC1.
∴D1E为D1B在平面D1DCC1上的射影,
∴∠BD1E为所求角.
在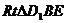 中,
中,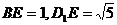 .
.
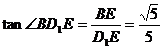 .
.
∴所求角为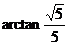 .
---------------------------------14分
.
---------------------------------14分
解法二:
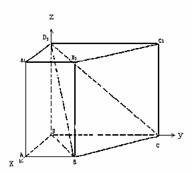 (I)证明:如图建立坐标系D-xyz,
(I)证明:如图建立坐标系D-xyz,
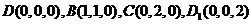 .
.
∴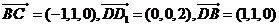 .
.
∵ ,
,
∴BC⊥DD1, BC⊥DB.
∵D1D∩ DB=D,
∴BC⊥平面D1DB. ------------------6分
(II) 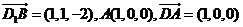 .
.
∵AD⊥平面D1DCC1,
∴平面D1DCC1的法向量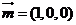 ,
,
∵ .
.
∴D1B与平面D1DCC1所成角的大小为 .
--------------------14分
.
--------------------14分
17.(北京市东城区2009年3月高中示范校高三质量检测文理)(本小题14分)
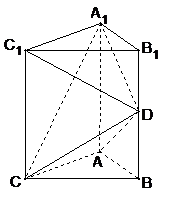 如图,直三棱柱
如图,直三棱柱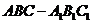 中,
中,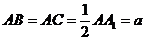 ,
, ,D为棱
,D为棱 的中点.
的中点.
(I)证明: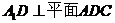 ;
;
(II)求异面直线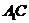 与
与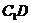 所成角的大小;
所成角的大小;
(III)求平面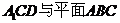 所成二面角的大小(仅考虑
所成二面角的大小(仅考虑
锐角情况).
17.(本小题14分)
(I)证: 都为等腰直角三角形
都为等腰直角三角形
 ,即
,即 …………………………………………… (2分)
…………………………………………… (2分)
又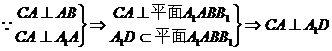
 ………………………………………………………… (4分)
………………………………………………………… (4分)
(II)解:连 交
交 于E点,取AD中点F,连EF、CF,则
于E点,取AD中点F,连EF、CF,则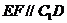
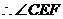 是异面直线
是异面直线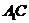 与
与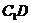 所成的角(或补角)………………… (5分)
所成的角(或补角)………………… (5分)
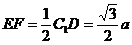 ,
,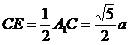 ,
,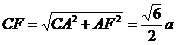
在 中,
中, ………………… (8分)
………………… (8分)
则异面直线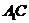 与
与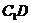 所成角的大小为
所成角的大小为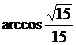 …………………… (9分)
…………………… (9分)
(III)解:延长 与AB延长线交于G点,连接CG
与AB延长线交于G点,连接CG
过A作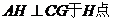 ,连
,连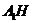 ,
,
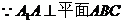 ,
, (三垂线定理)
(三垂线定理)
则 的平面角,即所求二面角的平面角… (10分)
的平面角,即所求二面角的平面角… (10分)
在直角三角形ACG中,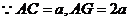
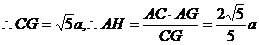 ………………………………(11分)
………………………………(11分)
在直角三角形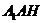 中,
中,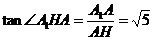 …………………… (13分)
…………………… (13分)
 ,
,
即所求的二面角的大小为 ……………………………………… (14分)
……………………………………… (14分)
得 分
评卷人
17. (北京市丰台区2009年3月高三统一检测理)(本小题共14分)
 如图,在正三棱柱
如图,在正三棱柱 中,
中, ,
, 是
是 的中点,点
的中点,点 在
在 上,
上,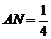 。
。
(Ⅰ)求 所成角的正弦值;
所成角的正弦值;
(Ⅱ)证明 ;
;
(Ⅲ) 求二面角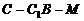 的大小.
的大小.
解:(Ⅰ)在正三棱柱 中,
中, 

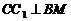 ,又
,又 是正△ABC边
是正△ABC边 的中点,
的中点,

 ,
,
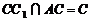


 ∠
∠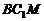 为
为 所成角
所成角
又 
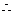 sin∠
sin∠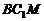 =
=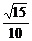 …………5分
…………5分
(Ⅱ)证明: 依题意得  ,
,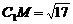 ,
,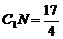
因为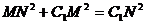
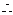
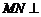
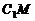 由(Ⅰ)知
由(Ⅰ)知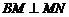 , 而
, 而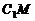
 ,
,
所以 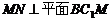 所以
所以 …………9分
…………9分
(Ⅲ) 过C作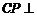
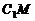 于
于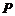 ,作
,作
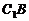 于
于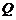 ,连接
,连接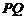


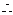
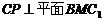 , …………11分
, …………11分
又

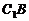
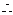
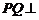
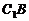
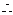
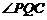 是所求二面角
是所求二面角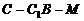 的平面角
的平面角

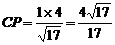 ,
,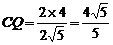
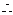
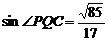
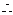 二面角
二面角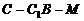 的大小为
的大小为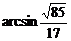 …………14分
…………14分
17. (北京市丰台区2009年3月高三统一检测文)(本小题共14分)
 如图,在正三棱柱
如图,在正三棱柱 中,
中, ,
, 是
是 的中点,点
的中点,点 在
在 上,
上,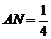 。
。
(Ⅰ)求 所成角的大小;
所成角的大小;
(Ⅱ)求二面角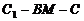 的正切值;
的正切值;
(Ⅲ) 证明 .
.
解:(Ⅰ)在正三棱柱 中,
中, 
又  是正△ABC
是正△ABC 边的中点,
边的中点,


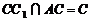

 …………3分
…………3分
 ∠
∠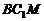 为
为 所成角
所成角
又 
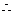 sin∠
sin∠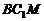 =
=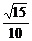 …………5分
…………5分
所以 所成角为
所成角为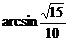 (
(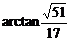 )
)
(Ⅱ) 由已知得 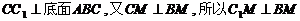
∠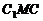 为二面角
为二面角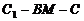 的平面角, 所以
的平面角, 所以 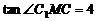 …………9分
…………9分
(Ⅲ)证明: 依题意 得  ,
,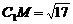 ,
,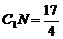
因为 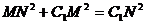
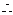
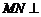
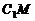 …………11分
…………11分
又由(Ⅰ)中 知
知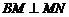 ,且
,且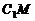
 ,
,
 …………14分
…………14分