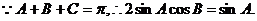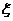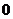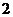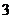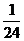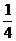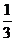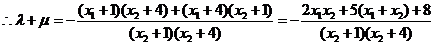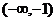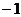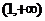17.(1)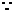
 ,
,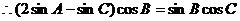 ,
,
即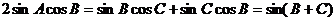 ……………………..3分
……………………..3分
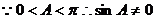 .
. 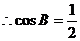 .
.
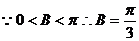 …………………………………………………………….6分
…………………………………………………………….6分
(2)m・n=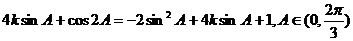 ,…..8分
,…..8分
设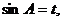 则
则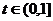 .
.
则m・n=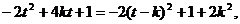
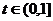 ……………………….10分
……………………….10分
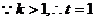 时,m・n取最大值.
时,m・n取最大值.
依题意得,(m・n) =
=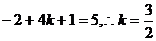 …………………………………12分
…………………………………12分
18.解:(Ⅰ)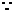 当
当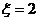 时,有
时,有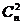 种坐法,
…………………………2分
种坐法,
…………………………2分
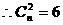 ,即
,即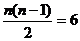 ,
,
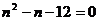 ,
,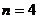 或
或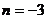 (舍去).
(舍去). 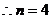 . ……………………4分
. ……………………4分
(Ⅱ)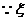 的可能取值是
的可能取值是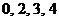 ,
,
又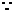
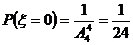 ,
, 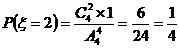 ,
,
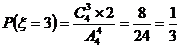 ,
,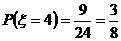 ,………………………8分
,………………………8分
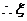 的概率分布列为:
的概率分布列为:
P
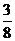
…………………10分
则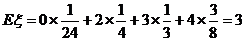 .
……………………12分
.
……………………12分
19.不妨设正三角形ABC 的边长为 3 .
(I)在图1中,取BE的中点D,连结DF.
∵AE EB=CF
EB=CF FA=1
FA=1 2,∴AF=AD=2,而∠A=600,
2,∴AF=AD=2,而∠A=600,
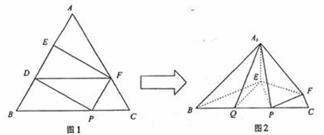 ∴△ADF是正三角形,又AE=DE=1,∴EF⊥AD…………2分
∴△ADF是正三角形,又AE=DE=1,∴EF⊥AD…………2分
在图2中,A1E⊥EF,BE⊥EF,
∴∠A1EB为二面角A1-EF-B的平面角
由题设条件知此二面角为直二面角,∴A1E⊥BE.
又BE∩EF=E,∴A1E⊥平面BEF,即A1E⊥平面BEP……….4分
(II)在图2中,∵A1E不垂直于A1B,∴A1E是平面A1BP的斜线.
又A1E⊥平面BEP, ∴A1E⊥BP,
从而BP垂直于A1E在平面A1BP内的射影(三垂线定理的逆定理).
设A1E在平面A1BP内的射影为A1Q,且A1Q交BP于点Q,则
∠EA1Q就是A1E与平面A1BP所成的角,…………………6分
且BP⊥A1Q.
在△EBP中,∵BE=BP=2,∠EBP=600, ∴△EBP是等边三角形,∴BE=EP.
又A1E⊥平面BEP,∴A1B=A1P,∴Q为BP的中点,且EQ=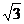
又A1E=1,在Rt△A1EQ ,tan∠EA1Q=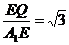 ,∴∠EA1Q=600.
,∴∠EA1Q=600.
所以直线A1E与平面A1BP所成的角为600…………………8分
(III)在图3中,过F作FM⊥A1P于M,连结QM,QF.
∵CF=CP=1, ∠C=600. ∴△FCP是正三角形,∴PF=1.
又PQ=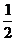 BP=1,∴PF=PQ.
①
BP=1,∴PF=PQ.
①
∵A1E⊥平面BEP,EQ=EF=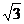 , ∴A
, ∴A
从而∠A1PF=∠A1PQ. ②
由①②及MP为公共边知 △FMP≌△QMP,
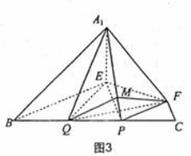 ∴∠QMP=∠FMP=900,且MF=MQ,
∴∠QMP=∠FMP=900,且MF=MQ,
从而∠FMQ为二面角B-A1P-F的平面角……………10分
在Rt△A1QP中,A1Q=A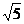 .
.
∵MQ⊥A1P, ∴MQ=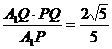 ,∴MF=
,∴MF=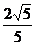 .
.
在△FCQ中,FC=1,QC=2,∠C=600,由余弦定理得QF=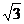 .
.
在△FMQ中,cos∠FMQ=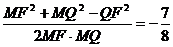
所以二面角B-A1P-F的大小为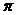 -arccos
-arccos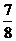 ……………..12分
……………..12分
20.解:(1)由条件得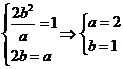 ,所以方程
,所以方程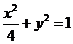 ………3分
………3分
(2)易知直线l斜率存在,令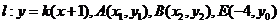
由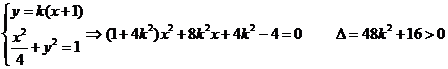
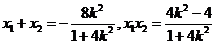 …………………6分
…………………6分
由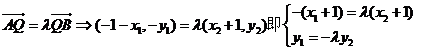
得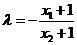 …………………8分
…………………8分
由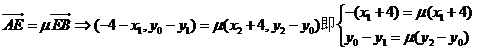
得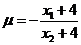 …………………10分
…………………10分
将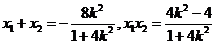 代入
代入
有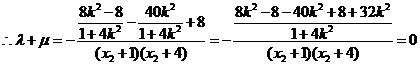 ……………12分
……………12分
21.(1)由题设得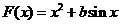 ,
,
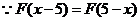 ,则
,则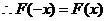 ,
,
所以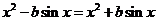 ……………………………………………………2分
……………………………………………………2分
所以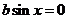 对于任意实数
对于任意实数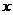 恒成立
恒成立
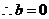 .故
.故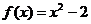 …………………………………………………………..3分
…………………………………………………………..3分
(2)由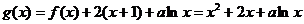 ,求导数得
,求导数得
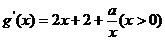 ,
,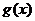 在
在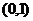 上恒单调,只需
上恒单调,只需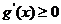 或
或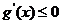 在
在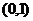 上恒成立,即
上恒成立,即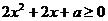 或
或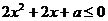 恒成立,所以
恒成立,所以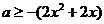 或
或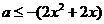 在
在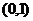 上恒成立…………………………………………………6分
上恒成立…………………………………………………6分
记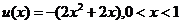 ,可知:
,可知: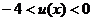 ,
,
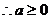 或
或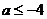 ………………………………………………………………….8分
………………………………………………………………….8分
(3)令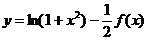 ,则
,则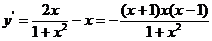 . 令
. 令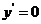 ,则
,则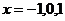 ,列表如下.
,列表如下.

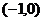
0
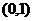
1
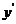
+
0
―
0
+
0
―
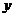
递增
极大值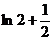
递减
极小值1
递增
极大值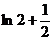
递减
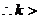
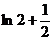 时,无零点;
时,无零点;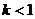 或
或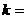
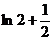 时,有两个零点;
时,有两个零点;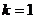 时有三个零点;
时有三个零点;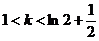 时,有四个零点…………………………………………………………12分
时,有四个零点…………………………………………………………12分
22.(1)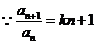 ,
,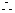
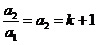 ………………………………….1分
………………………………….1分
又因为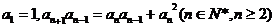 ,则
,则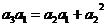 ,即
,即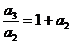 ,又
,又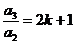 ,
,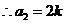 ,
,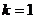 …………………………………….4分
…………………………………….4分
(2)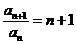 ,
,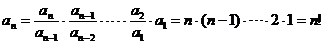 …….5分
…….5分
因为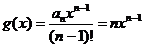 ,所以
,所以
当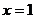 时,
时,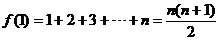
当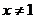 时,
时,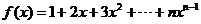 ,①
,①
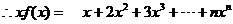 ,②
,②
①-②: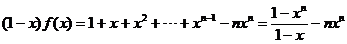 ,……………8分
,……………8分
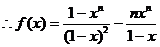 .综上所述,
.综上所述,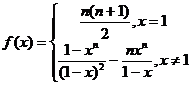 ……………9分
……………9分
(3)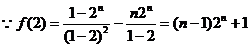 ,…………………………………..10分
,…………………………………..10分
又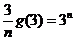 ,易验证当
,易验证当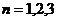 时不等式成立;…………………………………11分
时不等式成立;…………………………………11分
假设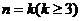 ,不等式成立,即
,不等式成立,即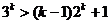 ,两边乘以3得
,两边乘以3得
又因为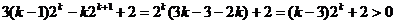
所以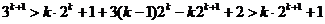
即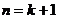 时不等式成立.故不等式恒成立……………………………………………..14分
时不等式成立.故不等式恒成立……………………………………………..14分