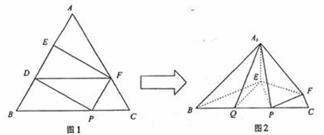
∴△ADF是正三角形，又AE=DE=1，∴EF⊥AD…………2分

在图2中，A₁E⊥EF，BE⊥EF，

∴∠A₁EB为二面角A₁-EF-B的平面角

由题设条件知此二面角为直二面角，∴A₁E⊥BE.

又BE∩EF=E，∴A₁E⊥平面BEF，即A₁E⊥平面BEP……….4分

(II)在图2中，∵A₁E不垂直于A₁B，∴A₁E是平面A₁BP的斜线.

又A₁E⊥平面BEP, ∴A₁E⊥BP,

从而BP垂直于A₁E在平面A₁BP内的射影（三垂线定理的逆定理）.

设A₁E在平面A₁BP内的射影为A₁Q，且A₁Q交BP于点Q，则

∠EA₁Q就是A₁E与平面A₁BP所成的角，…………………6分

且BP⊥A₁Q.

在△EBP中，∵BE=BP=2，∠EBP=60⁰，  ∴△EBP是等边三角形，∴BE=EP.