1. 甲、乙两人独立地解同一个问题,甲解决这个问题的概率是 ,乙解决这个问题的概率是
,乙解决这个问题的概率是 ,那么甲、乙中至少有一人解决这个问题的概率是( )
,那么甲、乙中至少有一人解决这个问题的概率是( )
(A)  (B)
(B)
 (C)
(C)
 (D)
(D) 
2. 5个人分4张同样的门票,每人至多分1张,而且票必须分完,记不同的分法种数为m;4个人分5张同样的门票,每人至少分1张,而且票必须分完,记不同的分法种数为n,则( )
(A) m > n (B) m < n (C) m = n (D) m、n的大小关系不确定
3. 把a,a,b,c,d五个字母排成一行,两个字母a不相邻的排列数为( )
(A) 96 (B) 72 (C) 60 (D) 36
4. 用一个平面去截正方体,所得的截面不可能是 ( )
(A)直角三角形 (B)对角线不相等的菱形 (C)梯形 (D)五边形
 5. 如右图,棱锥P―ABCDEF的底面是正六边形,侧棱PA垂直于底面,则下列命题正确的是 ( )
5. 如右图,棱锥P―ABCDEF的底面是正六边形,侧棱PA垂直于底面,则下列命题正确的是 ( )
(A) ∠PEA >∠PEF
(B) PC的长是点P到直线CD的距离
(C) EC的长是点E到平面PBC的距离
(D) ∠PDA是侧面PDE与底面所成二面角的平面角
6. 已知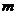 、
、 是直线,
是直线, 、
、 、
、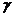 是平面,有下列五个命题:
是平面,有下列五个命题:
①若 ,
, ,
, ,则
,则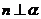 或
或 ;
;
②若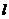 ⊥
⊥ ,
,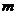

 ,
,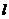 ⊥
⊥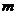 ,则
,则 ∥
∥ ;
;
③若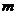 不垂直于
不垂直于 ,则
,则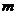 不可能垂直于
不可能垂直于 内的无数条直线;
内的无数条直线;
④若 ,
,
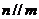 ,且
,且 ,
, ,则
,则 且
且 ;
;
⑤若 ,
, ,
, ,则
,则 或
或 .
.
其中真命题的个数是( )
(A) 1 (B) 2 (C) 3 (D) 4
7. 四面体的六条棱中,有五条棱长都等于a,记第六条棱与其对棱之间的距离为d,该四面体的体积为V,则 ( )
(A) d、V均有最大值 (B) d、V均无最大值
(C) d无最大值、V有最大值 (D) d有最大值、V无最大值
8. 在一个半径为R的半球内有一内接圆柱,圆柱的一个底面落在半球的大圆面上,则这个圆柱的侧面积的最大值为( )
(A)  (B)
(B)
 (C)
(C)
 (D)
(D)

9. 连续地同时抛掷两枚骰子,当第3次出现两枚点数之和是4的倍数时恰好抛掷了6次的概率是( )
(A)  (B)
(B)  (C)
(C)
 (D)
(D) 
10. 将4个相同的红球和4个相同的蓝球排成一排,从左到右每个球依次对应的序号为1,2,…,8,若同色球之间不区分,则4个红球对应的序号之和小于4个蓝球对应的序号之和的不同排列方法种数为( )
(A) 27 (B) 31 (C) 54 (D) 62
11.设 ,则
,则 ;
;
12. 如图,多面体是经过正四棱柱底面顶点B作截面 而截得的,且
而截得的,且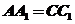 ,已知截面
,已知截面 与底面ABCD成
与底面ABCD成 的二面角,AB = 1, 则这个多面体的体积为
;
的二面角,AB = 1, 则这个多面体的体积为
;
 13. 在棱长为a的正方体内有内切球一个,过正方体中两条异面的棱的中点作直线,该直线与球面交于两点,则这两点间的球面距离为
;
13. 在棱长为a的正方体内有内切球一个,过正方体中两条异面的棱的中点作直线,该直线与球面交于两点,则这两点间的球面距离为
;
14. 如图,把正五边形ABCDE的五个顶点染上红、黄、蓝、绿四种颜色中的一种,要求相邻顶点所染颜色不相同,且四种颜色都要用到,则不同的染色方法一共有 种;
15. 不透明的箱内有编号分别为1,2,…,9的九个球,每次随机取出一个,记录其编号后放回箱中,以 表示前n次取球的编号总和为偶数的概率,则
表示前n次取球的编号总和为偶数的概率,则 .
.
16.(本小题满分12分)某大楼共5层,4个人从第一层上电梯,假设每个人都等可能地在每一层下电梯,并且他们下电梯与否相互独立,又知电梯只有在有人下时才停止.
(1) 求恰有2人在第二层下电梯的概率;
(2) 求电梯停下的次数不超过3次的概率.
17.(本小题满分12分)现有“掷骰子放小球”的游戏规定:若掷出1点,则在甲盒中放入一个球;若掷出2点或3点,则在乙盒中放入一个球;若掷出4点、5点或6点,则在丙盒中放入一个球. 设掷骰子n次后,甲、乙、丙各盒内球数分别为x、y、z.
(1) 当n=6时,求y>4的概率;
(2) 当n=3时,求x、y、z成等差数列的概率.
 18.(本小题满分12分)如图, P是正四棱柱
18.(本小题满分12分)如图, P是正四棱柱 的底面
的底面 的中心,,E是AB的中点,
的中心,,E是AB的中点,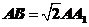 .
.
(1) 求证: 平面
平面 ;
;
(2) 求直线PA与平面PBC所成角的大小.
19.(本小题满分12分)如图,已知 是正三角形,E、F分别是AC、AB的中点,将
是正三角形,E、F分别是AC、AB的中点,将 折起,记折起后点A所在位置为点P,且使得
折起,记折起后点A所在位置为点P,且使得 .
.
(1) 求证: 平面
平面 ;
;
 (2)
求二面角
(2)
求二面角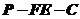 的大小;
的大小;
20.(本小题满分13分)如图, 已知直三棱柱 的侧棱长为2,底面△ABC是等腰直角三角形, 且∠ACB
= 90°,AC =
2, F为棱
的侧棱长为2,底面△ABC是等腰直角三角形, 且∠ACB
= 90°,AC =
2, F为棱 的中点.
的中点.
(1) 求证:平面 平面
平面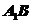 ;
;
(2) 求异面直线 和
和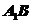 所成的角;
所成的角;
(3) 若E为AB上一点, 试确定点E在AB上的位置, 使得 ;并求此时点A到平面
;并求此时点A到平面 的距离.
的距离.
21.(本小题满分14分)解答下列问题:
(1) 已知 .
.
① 若n=12,求f(x)的展开式中的常数项及展开式的项数;
② 若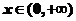 ,求函数f(x)的最小值及相应x的值.
,求函数f(x)的最小值及相应x的值.
(2) 将100名跳棋选手分成12个小组,举行三人跳棋比赛,各小组内每三人比赛一场,不在同一小组的棋手不比赛.
① 证明:对于任何两个小组,在总人数一定的情况下,当它们的人数至多相差为1时,总的比赛场数最少;
② 请给出一种分组方案,使得比赛总场数最少;并求出最少的比赛总场数.
武汉外国语学校2008――2009学年度下学期期中考试




