13.设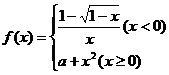 ,要使函数
,要使函数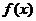 在
在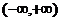 内连续,则
内连续,则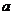 的值为
.
的值为
.
14.设等差数列{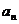 },{
},{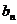 }的前
}的前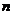 项的和分别为
项的和分别为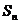 与
与 ,若
,若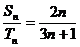 ,则
,则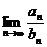 =
.
=
.
15.利用数学归纳法证明(n+1)(n+2)…(n+n)=2n・1・3・…・(2n-1)时,由k到k+1左边应添加的因式是 .
16.函数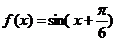 的图象按向量
的图象按向量 平移后得到
平移后得到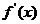 的图象,其中
的图象,其中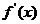 为
为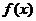 的导函数,且
的导函数,且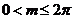 ,则
,则 .
.
17.(本小题满分10分)甲、乙两篮球运动员进行定点投篮,每人各投4个球,甲投篮命中的概率为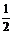 ,乙投篮命中的概率为
,乙投篮命中的概率为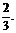
(Ⅰ)求甲至多命中2个且乙至少命中2个的概率;
(Ⅱ)若规定每投篮一次命中得3分,未命中得-1分,求乙所得分数η的概率分布和数学期望.
18.(本小题满分12分)有一个4×5×6的长方体, 它的六个面上均涂上颜色. 现将这个长方体锯成120个1×1×1的小正方体,从这些小正方体中随机地任取1个.
(Ⅰ)设小正方体涂上颜色的面数为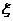 ,求
,求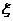 的分布列和数学期望.
的分布列和数学期望.
(Ⅱ)如每次从中任取一个小正方体,确定涂色的面数后,再放回,连续抽取6次,设恰好取到两面涂有颜色的小正方体次数为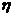 . 求
. 求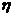 的数学期望.
的数学期望.
19.(本小题满分12分)盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球,规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得?1分.现从盒中任取3个球,(Ⅰ)求取出的3个球颜色互不相同的概率;
(Ⅱ)求取出的3个球得分之和恰为1分的概率;
(Ⅲ)设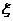 为取出的3个球中白色球的个数,求
为取出的3个球中白色球的个数,求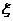 的分布列和数学期望.
的分布列和数学期望.
20.(本小题满分12分)
用长为90cm、宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边形翻转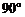 ,再焊接而成(如图),问该容器的高为多少时,容器的容积最大?
,再焊接而成(如图),问该容器的高为多少时,容器的容积最大?
21.(本小题满分12分)已知函数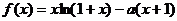 ,其中a为常数.
,其中a为常数.
(Ⅰ)若当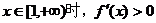 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(Ⅱ)求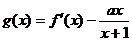 的单调区间.
的单调区间.
22.(本小题满分12分)已知函数 在点
在点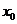 处取得极小值-4,使其导数
处取得极小值-4,使其导数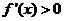 的
的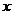 的取值范围为
的取值范围为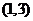 ,求:(1)
,求:(1)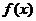 的解析式;
的解析式;
(2)若过点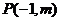 可作曲线
可作曲线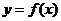 的三条切线,求实数
的三条切线,求实数 的取值范围.
的取值范围.

 郑州四中2008――2009学年高三理科数学第一次调考答题卷
郑州四中2008――2009学年高三理科数学第一次调考答题卷
一.选择题(本大题12小题,每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
13.________________; 14.____________ ; 15. _____________; 16. _______________.
 17.解:
17.解:
 18.解:
18.解:
 19.解:
19.解:
|

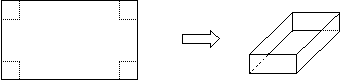
 20.解:
20.解: 21.解:
21.解: 22.解:
22.解:
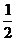 . 14.
. 14.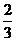 .
15.
.
15.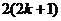 .
16.
.
16.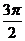 .
.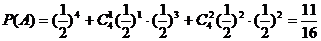 …………………………2分
…………………………2分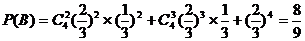 …………………………………4分
…………………………………4分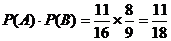 …………………………………………5分
…………………………………………5分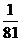
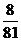
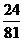
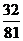
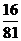
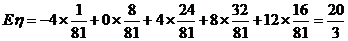 ………………………10分
………………………10分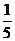
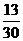
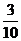
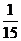
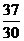
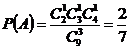 .(3分)
.(3分)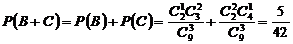 .(6分)
.(6分)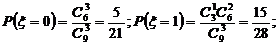
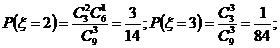

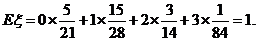 .(12分)
.(12分)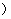 .
.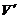 (x) = 12x2-552x + 4320
(x) = 12x2-552x + 4320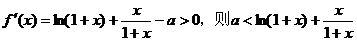 ……………2分
……………2分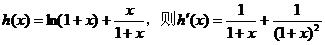
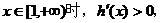 ∴
∴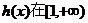 上单调递增,
上单调递增,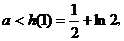 ∴a的取值范围是
∴a的取值范围是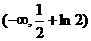 ………………………6分
………………………6分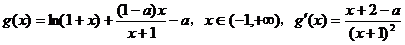
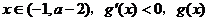 是减函数;
是减函数;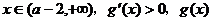 是增函数 ……………………………………8分
是增函数 ……………………………………8分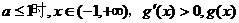 是增函数 …………………………10分
是增函数 …………………………10分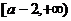 ,减区间为
,减区间为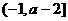 ,
,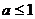 时,增区间为
时,增区间为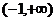 …………………………………………………12分
…………………………………………………12分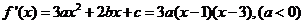
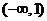 上
上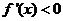 ;在
;在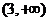 上
上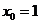 处取得极小值
处取得极小值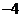
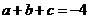 ①
①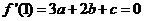 ②
②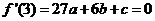 ③
③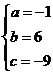
 (7分)
(7分)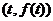
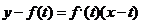
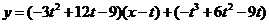

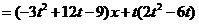 过
过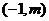
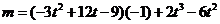
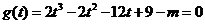
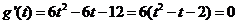 ,
,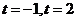 ,方程
,方程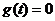 有三个根。
有三个根。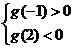
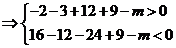
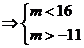
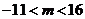
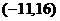 (12分)
(12分)