1.下列说法正确的是 ( )
A.一个命题的逆命题为真,则它的否命题为假
B.一个命题的逆命题为真,则它的逆否命题为真
C.一个命题的逆否命题为真,则它的否命题为真
D.一个命题的否命题为真,则它的逆命题为真
2.双曲线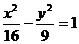 的渐近线方程为 ( )
的渐近线方程为 ( )
A.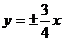 B.
B.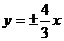 C.
C. D.
D.
3.已知p是r的充分不必要条件,s是r的必要条件,q是s的必要条件,那么p是q成立的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.抛物线 的准线方程为 ( )
的准线方程为 ( )
A.x=1 B.x=
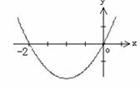 5.函数
5.函数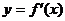 的图象如图所示,则
的图象如图所示,则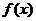 的解析式可能是 ( )
的解析式可能是 ( )
A. B.
B.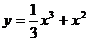
C.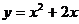 D.
D.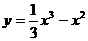
6.如果质点A按规律s=3t2运动,则在t=2时的瞬时速度是 ( )
A.4 B.6 C.12 D.24
7.平面内有一长度为2的线段AB和一动点P,若满足|PA|+|PB|=8,则|PA|的取值范围是
( )
A.[1,4] B.[2,6] C.[3,5 ] D. [3,6]
8.函数f(x)=x3-ax+1在区间(1,+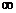 )内是增函数,则实数a的取值范围是
)内是增函数,则实数a的取值范围是
( )
A.a<3 B.a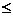 3 C.a>3 D.a
3 C.a>3 D.a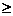 3
3
9.过抛物线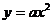 (a>0)的焦点F的一条直线交抛物线于P、Q两点,若线段PF和FQ的长分别是p、q,则
(a>0)的焦点F的一条直线交抛物线于P、Q两点,若线段PF和FQ的长分别是p、q,则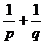 等于 ( )
等于 ( )
A.2a B.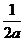 C.4a D.
C.4a D.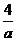
10.椭圆有如下光学性质,从椭圆的一个焦点出发的光线,经椭圆反射后必过椭圆的另一个焦点。现有一水平放置的椭圆形台球盘,点A,B是它的两个焦点,其长轴长为2a,焦距为2c(a>c>0),静放在点A的点光源发出的光线经椭圆壁反射后,第一次回到点A时,光线经过的路程为 ( )
A.2(a+c) B.2(a-c) C.4a D.均有可能
第Ⅱ卷
11.函数f(x)=sinx-cosx的导函数为________________.
12.已知椭圆经过(0,2)和(1,0),则椭圆的标准方程为_____________________________.
13.已知函数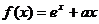 在点
在点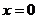 处有极值,则a=__________________.
处有极值,则a=__________________.
14.曲线 在x=3处的切线方程是____________________.
在x=3处的切线方程是____________________.
15.已知命题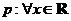 ,
, ,则
,则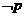 是_____________________.
是_____________________.
16.若点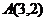 ,
,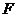 为抛物线
为抛物线 的焦点,点
的焦点,点 在抛物线上移动,则使
在抛物线上移动,则使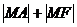 取最小值时,点
取最小值时,点 的坐标是
.
的坐标是
.
17.给出问题:F1、F2是双曲线 的焦点,点P在双曲线上。若点P到焦点F1的距离等于9,求点P到焦点F2的距离。某学生的解答如下:双曲线的实轴长为8,由||PF1|-|PF2||=8,即|9-|PF2||=8,得|PF2|=1或17。该学生的解答是否正确?若正确,请将他的解题依据填在下面横线上,若不正确,将正确结果填在横线上。_____________________________________________.
的焦点,点P在双曲线上。若点P到焦点F1的距离等于9,求点P到焦点F2的距离。某学生的解答如下:双曲线的实轴长为8,由||PF1|-|PF2||=8,即|9-|PF2||=8,得|PF2|=1或17。该学生的解答是否正确?若正确,请将他的解题依据填在下面横线上,若不正确,将正确结果填在横线上。_____________________________________________.
18.(本小题满分12分)
已知双曲线与椭圆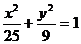 共焦点,它们的离心率之和为
共焦点,它们的离心率之和为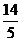 ,求双曲线的标准方程。
,求双曲线的标准方程。
19.(本小题满分14分)
已知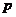 :方程
:方程 表示双曲线;
表示双曲线;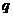 :函数
:函数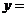
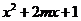 与
与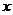 轴无公共点,若
轴无公共点,若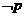 和
和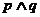 都是假命题,求实数
都是假命题,求实数 的取值范围.
的取值范围.
20.(本小题满分15分)
如图,椭圆的标准方程为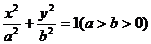 ,P为椭圆上的一点,且满足
,P为椭圆上的一点,且满足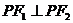 ,
,
(1)求三角形PF1F2的面积。
 (2)若此椭圆长轴为8,离心率为
(2)若此椭圆长轴为8,离心率为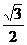 ,求点P的坐标。
,求点P的坐标。
21.(本小题满分15分)
设函数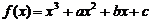 ,已知它在x= -2时有极值,且过曲线
,已知它在x= -2时有极值,且过曲线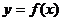 上的点
上的点 的切线方程为
的切线方程为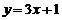 .
.
(1)求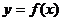 的表达式;
的表达式;
(2)若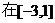 上
上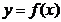 满足f(x)<m恒成立,求m的取值范围.
满足f(x)<m恒成立,求m的取值范围.
22.(本小题满分16分)
已知抛物线C: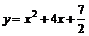 ,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.
,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.
(1)若C在点M的法线的斜率为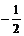 ,求点M的坐标(x0,y0);
,求点M的坐标(x0,y0);
(2)设P(-2,a)为C对称轴上的一点,在C上是否存在点,使得C在该点的法线通过点P?若有,求出这些点,以及C在这些点的法线方程;若没有,请说明理由.
杭绍金温衢七校2008学年第二学期期中联考答题卷
 高二数学(文科)
高二数学(文科)
座位号:
题号
一
二
18
19
20
21
22
总分
得分
评卷人
题号
1
2
3
4
5
6
7
8
9
10
答案
11.____________________ 12._____________________
13.____________________ 14._____________________
15.____________________ 16._____________________
17.____________________
 18.
18.
 19.
19.
20.
 |
|||
 |
|||
21.

22.

杭绍金温衢七校2008学年第二学期期中联考

