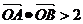1.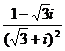
A.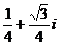 B.
B.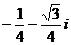 C.
C.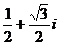 D.
D.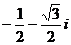
2.已知函数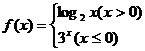 ,则
,则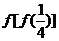 的值是
的值是
A. 9 B.
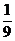 C.-9 D.-
C.-9 D.-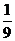
3.下列函数中,图象与函数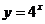 的图象关于
的图象关于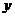 轴对称的是
轴对称的是
A. 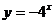 B.
B. 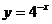 C.
C. 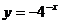 D.
D. 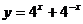
4.下列函数中值域是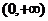 的函数是
的函数是
A.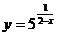 B.
B. 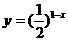 C.
C. 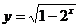 D.
D.
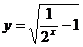
5.已知函数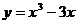 ,则它的单调增区间是
,则它的单调增区间是
A. 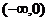 B.
B.
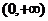 C.
C. 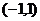 D.
D.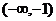 和
和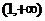
6.已知实数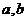 满足
满足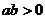 ,则代数式
,则代数式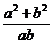 的值
的值
A.有最小值但没有最大值 B.有最大值但没有最小值
C.既有最大值也有最小值 D.没有最大值也没有最小值
7.若数列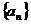 的前8项的值互异,且
的前8项的值互异,且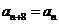 对任意的
对任意的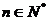 都成立,则下列数列中可取遍
都成立,则下列数列中可取遍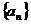 的前8项值的数列为
的前8项值的数列为
A. 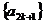 B.
B.
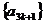 C.
C.
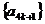 D.
D.
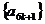
8.直线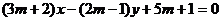 必过定点
必过定点
A.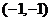 B.
B.
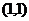 C.
C. 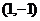 D.
D. 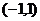
9..现从某校5名学生中选出3分别参加高中“数学”“物理”“化学”竞赛,要求每科至少有1人参加,且每人只参加1科竞赛,则不同的参赛方案的种数是 ;
11.若关于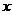 的方程
的方程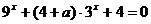 有解,则实数
有解,则实数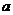 的取值范围是 ;
的取值范围是 ;
12.已知函数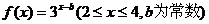 的图象经过点(2,1),则函数
的图象经过点(2,1),则函数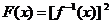
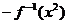 的值域为 ;
的值域为 ;
13. 某气象站天气预报准确率是80%,5次预报中至少有4次准确的概率是______(精确到0.01);
14、▲选做题:在下面三道题中选做两题,三题都选的只计算前两题的得分。
①若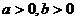 ,则
,则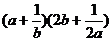 的最小值是
;
的最小值是
;
② 极坐标方程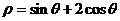 所表示的曲线是 ;
所表示的曲线是 ;
③在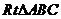 中,
中,
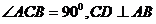 于点
于点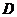 ,
,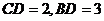 ,则
,则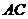 = ;
= ;
15.(本小题满分12分)
已知10件产品中有2件是次品.
(1)任意取出4件产品作检验,求其中恰有1件是次品的概率.
(2)为了保证使2件次品全部检验出的概率超过0.6,至少应抽取几件产品作检验?
16.(本小题满分12分)
已知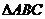 中,三内角
中,三内角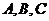 满足
满足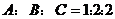 ,求
,求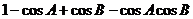 的值.
的值.
17.(本小题满分14分)
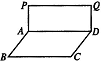
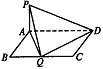
如图,矩形 与
与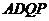 所在平面垂直,将矩形
所在平面垂直,将矩形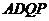 沿
沿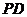 对折,使得翻折后点
对折,使得翻折后点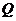 落在
落在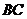 上,设
上,设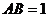 ,
,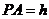 ,
,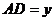 .
.
(1)试求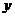 关于
关于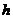 的函数解析式;
的函数解析式;
(2)当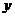 取最小值时,指出点
取最小值时,指出点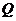 的位置,并求出此时
的位置,并求出此时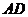 与平面
与平面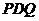 所成的角;
所成的角;
(3)在条件(2)下,求三棱锥P-ADQ内切球的半径。
18.(本小题满分14分)
等比数列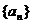 的首项为
的首项为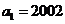 ,公比
,公比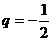 .
.
(1) 设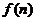 表示该数列的前
表示该数列的前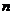 项的积,求
项的积,求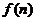 的表达式;
的表达式;
(2) 当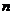 取何值时,
取何值时,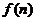 有最大值.
有最大值.
19.(本小题满分为14分)
已知函数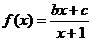 的图象过原点,且关于点
的图象过原点,且关于点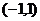 成中心对称.
成中心对称.
(1) 求函数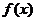 的解析式;
的解析式;
(2) 若数列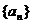 满足:
满足: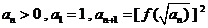 ,求
,求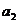 ,
,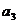 ,
,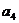 的值,猜想数列
的值,猜想数列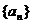 的通项公式
的通项公式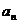 ,并证明你的结论;
,并证明你的结论;
(3) 若数列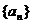 的前
的前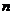 项和为
项和为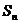 ,判断
,判断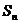 与2的大小关系,并证明你的结论.
与2的大小关系,并证明你的结论.
20.(本小题满分14分)
已知函数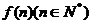 ,满足条件:
,满足条件:
①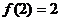 ;②
;② 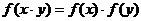 ;③
;③ 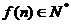 ;④当
;④当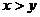 时,有
时,有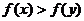 .
.
(1) 求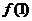 ,
,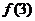 的值;
的值;
(2) 由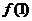 ,
,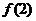 ,
,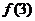 的值,猜想
的值,猜想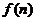 的解析式;
的解析式;
(3) 证明你猜想的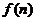 的解析式的正确性.
的解析式的正确性.
(二)
1.含有三个实数的集合可以表示为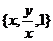 ,也可以表示为
,也可以表示为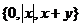 ,则
,则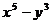 的值为
的值为
A. -1 B.
2.如果复数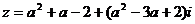 为纯虚数,那么实数
为纯虚数,那么实数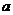 的值为
的值为
A. - 2 B.
3.在等差数列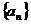 中,
中,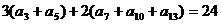 ,则此数列前13项的和是 A.13 B.
,则此数列前13项的和是 A.13 B.
4.编号为1、2、3、4、5的五个人分别去坐编号为1、2、3、4、5的五个座位,其中有且只有两个人的编号与座位号一致的坐法有
 A.10种 B.20种 C.30种 D.60种
A.10种 B.20种 C.30种 D.60种
5.若函数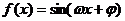 (
(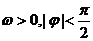 )的部分图象如图所示,则有
)的部分图象如图所示,则有
A.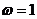
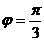 B.
B.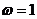

C.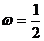
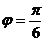 D.
D.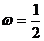
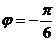
6.某工厂生产产品,用传送带将产品放入下一工序,质检人员每隔t分钟在传进带上某一固定位置取一件检验,这种抽样方法是
A . 简单抽样 B. 分层抽样 C. 系统抽样 D. 以上都不对
7. 设有如下三个命题:甲:相交直线 、
、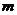 都在平面
都在平面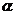 内,并且都不在平面
内,并且都不在平面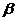 内;乙:直线
内;乙:直线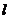 、
、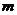 中至少有一条与平面
中至少有一条与平面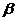 相交;丙:平面
相交;丙:平面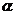 与平面
与平面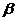 相交.
相交.
当甲成立时,
A.乙是丙的充分而不必要条件 B.乙是丙的必要而不充分条件
C.乙是丙的充分且必要条件 D.乙既不是丙的充分条件又不是丙的必要条件
8.现代社会对破译密码的难度要求越来越高。有一种密码把英文的明文(真实文)按字母分解,其中英文的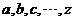 的26个字母(不论大小写)依次对应1,2,3,…,26这26个自然数(见下表):
的26个字母(不论大小写)依次对应1,2,3,…,26这26个自然数(见下表):
a
b
c
d
e
f
g
h
i
j
k
l
m
n
o
p
q
r
s
t
u
v
w
x
y
z
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
现给出一个变换公式: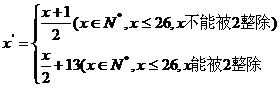 将明文转换成密文,如
将明文转换成密文,如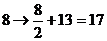 ,即
,即 变成
变成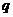 ;
; 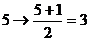 ,即
,即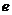 变成
变成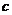 。按上述规定,若将明文译成的密文是shxc,那么原来的明文是
。按上述规定,若将明文译成的密文是shxc,那么原来的明文是
A. lhho B.love C.ohhl D.eovl
9.函数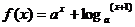 在
在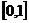 上的最大值与最小值之和为
上的最大值与最小值之和为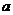 ,则
,则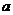 的值为 。
的值为 。
10.编辑一个运算程序: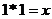 ,
,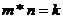 ,
,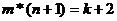 ,欲得到
,欲得到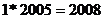 的输出结果,则
的输出结果,则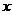 的值为 。
的值为 。
11.过抛物线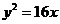 的焦点的直线l交抛物线于A、B两点,则
的焦点的直线l交抛物线于A、B两点,则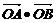 的值
的值
为 。
12.若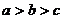 ,
,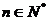 ,且
,且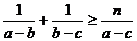 恒成立,则
恒成立,则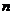 的最大值是 。
的最大值是 。
13.设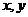 满足条件
满足条件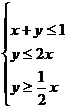 ,则目标函数
,则目标函数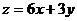 的最大值为 。
的最大值为 。
14、▲选做题:在下面三道题中选做两题,三题都选的只计算前两题的得分。
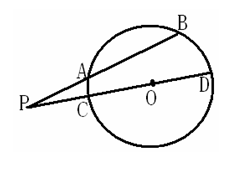
(1)如图,圆O的直径AB的延长线与弦CD的
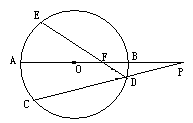 延长线相交于点P,E为圆O上一点,弧AE=弧AC,
延长线相交于点P,E为圆O上一点,弧AE=弧AC,
DE交AB于点F,且AB=2BP=4,则PF= 。
(2)设双曲线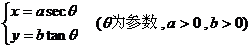 的右焦点为F,右准线
的右焦点为F,右准线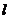 与两条渐线交于P、Q两点,如果△PQF是直角三角形,则双曲线的离心率e= 。
与两条渐线交于P、Q两点,如果△PQF是直角三角形,则双曲线的离心率e= 。
(3)函数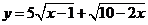 的最大值是
。
的最大值是
。
15.(本小题满分13分)已知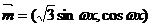 ,
,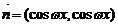 ,
,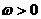 ,记函数
,记函数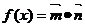 ,若函数
,若函数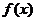 的最小正周期为
的最小正周期为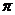 。
。
(1) 求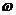 ;
;
(2) 当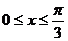 时,试求
时,试求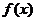 的值域。
的值域。
16.(本小题满分13分)
设飞机A有两个发动机,飞机B有四个发动机,如有半数或半数以上的发动机没有故障,飞机就能安全飞行。现设各发动机发生故障的概率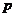 是
是 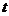 的函数
的函数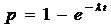 ,其中
,其中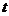 为发动机启动后所经历的时间,
为发动机启动后所经历的时间,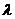 为正常数,试论证飞机A与飞机B哪一个安全(这里不考虑其他故障)。
为正常数,试论证飞机A与飞机B哪一个安全(这里不考虑其他故障)。
17.(本小题满分14分)
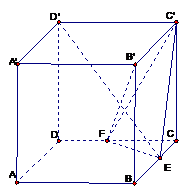
在棱长为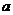 的正方体
的正方体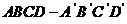 中,E、F分别是棱
中,E、F分别是棱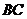 、
、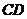 上的点,且
上的点,且
|


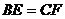 ;
;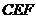 的面积取得最大值时,
的面积取得最大值时,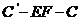 的余弦值。
的余弦值。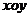 平面上有一系列的点
平面上有一系列的点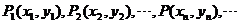 ,对于正整数
,对于正整数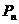 位于函数
位于函数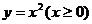 的图象上,以点
的图象上,以点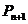 又彼此外切,若
又彼此外切,若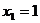 ,且
,且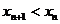 。
。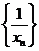 是等差数列;
是等差数列;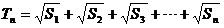 ,求证:
,求证: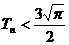
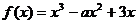

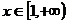 是增函数,求实数
是增函数,求实数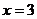 是
是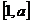 的最小值和最大值。
的最小值和最大值。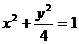 ,过点
,过点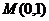 的直线
的直线 ,
, 是坐标原点,点
是坐标原点,点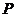 满足
满足 ,点
,点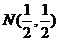 。当
。当 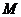 旋转时,求:
旋转时,求: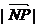 的最大值和最小值。
的最大值和最小值。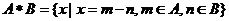 ,若A={4,5,6},B={1,2,3},则集合
,若A={4,5,6},B={1,2,3},则集合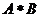 中的所有元素之和为
中的所有元素之和为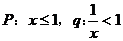 ,则非
,则非 是
是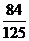 B.
B. 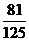 C.
C. 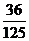 D.
D. 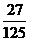
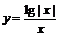 的图象大致是
的图象大致是 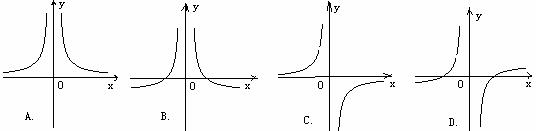
 ,向量
,向量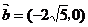 ,则
,则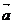 与
与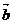 的夹角是
的夹角是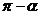 C.
C. 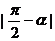 D.
D. 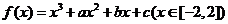 表示的曲线过原点,且在
表示的曲线过原点,且在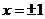 处的切线斜率均为-1,有以下命题
处的切线斜率均为-1,有以下命题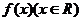 为奇函数,
为奇函数,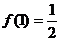 ,
,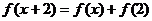 ,则
,则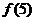 =
=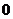 B.
B. 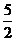 D. 5
D. 5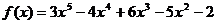 ,当
,当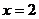 时的值,需要进行 次乘法运算及 次加(减)法运算。
时的值,需要进行 次乘法运算及 次加(减)法运算。 __
__。
__
__。 ,则
,则 是可导函数,且满足
是可导函数,且满足 则曲线
则曲线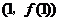 为切点的切线倾斜角
为切点的切线倾斜角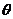 为 __ __。
为 __ __。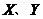 ,定义
,定义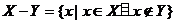 ,
,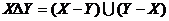
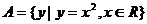 ,
,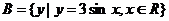 ,则
,则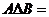 __ __。
__ __。
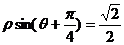 ,则点A
,则点A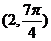 到这条直线的距离为_____________
到这条直线的距离为_____________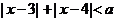 的解集不是空集,则参数
的解集不是空集,则参数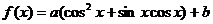
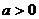 时,求
时,求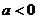 且
且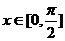 时,
时,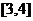 ,求
,求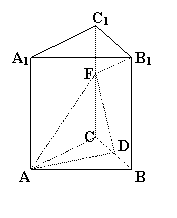 在三棱柱
在三棱柱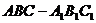 中,
中,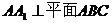
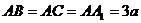 ,
,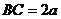 ,
,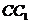 上一点,且
上一点,且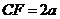 .
.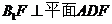 ;
;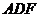 与平面
与平面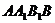 所成角的正弦值.
所成角的正弦值.
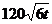 吨,其中
吨,其中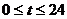 。
。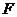 的直线交椭圆于
的直线交椭圆于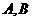 两点,
两点,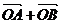 与
与 共线。
共线。 ,证明
,证明 为定值。
为定值。 。
。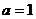 ,点
,点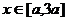 时,
时,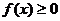 恒成立,求
恒成立,求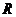 ,当
,当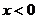 时,
时,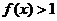 ,且对于任意的
,且对于任意的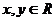 ,都有
,都有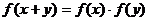 成立,数列
成立,数列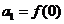 ,且
,且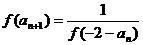 。
。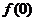 的值,并证明函数
的值,并证明函数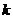 ,使
,使 对一切
对一切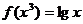 ,则
,则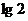 B.
B. 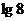 C.
C. 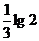 D.
D. 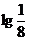
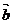 与向量
与向量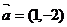 夹角为
夹角为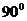 ,且
,且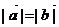 ,则
,则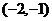 B、
B、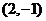 或
或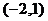 C、(2,1) D、
C、(2,1) D、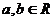 ,下列命题中正确的是
,下列命题中正确的是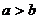 , 则
, 则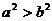 B. 若
B. 若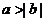 , 则
, 则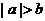 , 则
, 则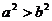 D. 若
D. 若 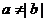 , 则
, 则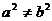
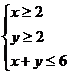 ,则
,则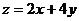 的最大值为
的最大值为 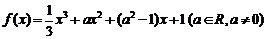 的导函数
的导函数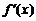 的图象,
的图象,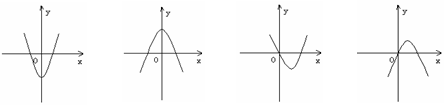
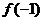 =
= 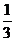 B.
B. 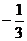 C.
C. 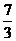 D.
D. 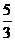
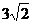 ,则这个四棱锥的外接球的表面积为
,则这个四棱锥的外接球的表面积为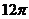 B.
B.  C.
C. 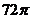 D.
D. 
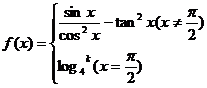 在点
在点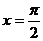 处连续,则实数
处连续,则实数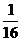 B.
B. 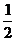 C.
1
D.2
C.
1
D.2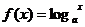 满足
满足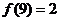 ,则
,则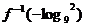 的值是
的值是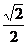 B.
B.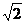 C.2 D.
C.2 D.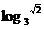
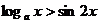 对于区间
对于区间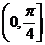 内的任意
内的任意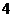 名大学生分配到3个企业去实习,不同的分配方案共有 种;如果每
名大学生分配到3个企业去实习,不同的分配方案共有 种;如果每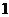 名学生,则不同的分配方案共有 种(用数字作答).
名学生,则不同的分配方案共有 种(用数字作答).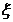 表示取得白子的个数,则E
表示取得白子的个数,则E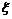 等于 ;
等于 ;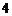 的等比数列
的等比数列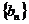 中,若
中,若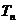 是数列
是数列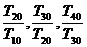 也成等比数列,且公比为
也成等比数列,且公比为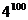 ;类比上述结论,相应地在公差为
;类比上述结论,相应地在公差为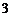 的等差数列
的等差数列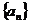 中,若
中,若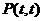
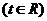 ,点
,点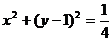 的动点,点N是圆
的动点,点N是圆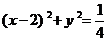 的动点,则
的动点,则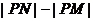 的最大值是 ;
的最大值是 ;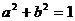 ,
,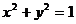 ,则
,则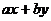 的取值范围是 ;
的取值范围是 ;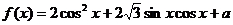 ,
,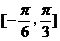 上最大值与最小值之和为3,求
上最大值与最小值之和为3,求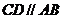 ,
,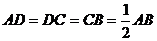 ,
,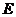 是
是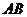 的中点,将
的中点,将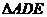 沿
沿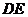 折起,使点
折起,使点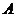 折到点
折到点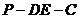 的大小为
的大小为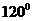 。
。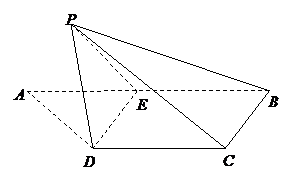 (1)求证:
(1)求证: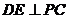 ;
;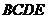 所成角的正弦值;
所成角的正弦值;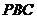 的距离。
的距离。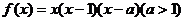
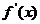 ,并证明
,并证明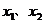 不等式
不等式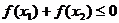 成立,求
成立,求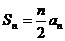 ,
,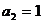 .
.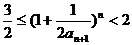 。
。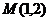 ,它们在
,它们在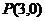 ,交抛物线于
,交抛物线于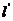 被以
被以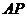 为直径的圆截得的弦长为定值?若存在,求出
为直径的圆截得的弦长为定值?若存在,求出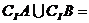
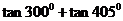 的值为
的值为
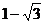 B.
B.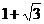 C.
C.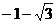 D.
D.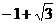
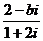 (其中i为虚数单位,b为实数)的实部和虚部互为相反数,那么b等于
(其中i为虚数单位,b为实数)的实部和虚部互为相反数,那么b等于
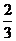 C.
C.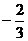 D.2
D.2 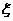 描述一次该项试验的成功次数,则
描述一次该项试验的成功次数,则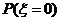 等于
等于
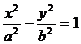
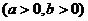 的离心率
的离心率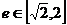 ,令双曲线两条渐近线构成的角中,以实轴为角平分线的角为
,令双曲线两条渐近线构成的角中,以实轴为角平分线的角为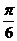 ,
,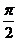 ]
B.[
]
B.[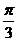 ,
,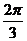 ]
D.[
]
D.[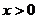 时,
时,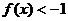 B.
B. 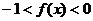 C.
C. 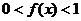 D.
D. 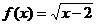 ,则
,则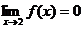 。
。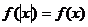 ;反之,也成立。
;反之,也成立。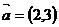 ,
,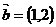 ,若
,若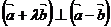 ,则
,则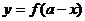 的图象和函数
的图象和函数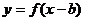 的图象关于直线
的图象关于直线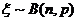 ,
,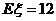 ,
,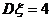 ,则
,则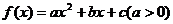 且方程
且方程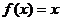 无实数根,则
无实数根,则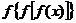 与
与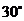 角,E,F分别是BC,AD的中点,则EF和AB所成的角是
。
角,E,F分别是BC,AD的中点,则EF和AB所成的角是
。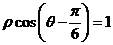 的直角坐标方程是 。
的直角坐标方程是 。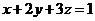 ,则
,则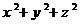 的最小值是 。
的最小值是 。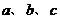 分别为角
分别为角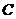 的对边.已知
的对边.已知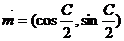 ,
,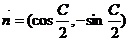 ,且
,且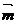 与
与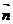 的夹角为
的夹角为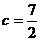 ,
,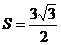 ,求
,求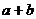 的值。
的值。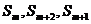 成等差数列,则
成等差数列,则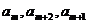 成等差数列。
成等差数列。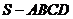 的底面是边长为4的正方形,
的底面是边长为4的正方形,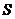 在底面上的射影
在底面上的射影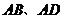 的距离分别为2、1。
的距离分别为2、1。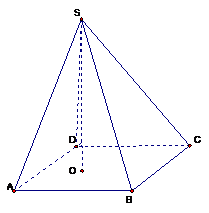
 的中点,且
的中点,且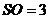 ,问在棱
,问在棱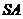 (不含端点)上是否存在一点
(不含端点)上是否存在一点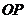 与
与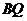 所成的角为
所成的角为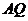 的长。
的长。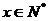 ,
,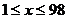 )的关系如下:
)的关系如下: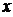
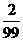
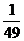
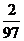
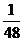
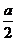 元。
元。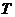 (元)表示为日产量
(元)表示为日产量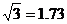 )
)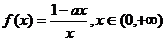 。设
。设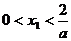 ,记曲线
,记曲线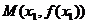 处的切线为
处的切线为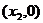 ,求证:
,求证: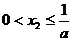 ; ② 若
; ② 若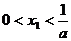 ,则
,则
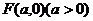 ,点
,点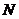 为动点,且
为动点,且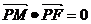 ,
,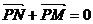
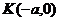 ,
,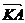 与
与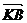 的夹角为
的夹角为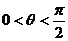 。
。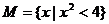 ,
,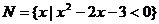 ,则集合
,则集合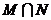 =
=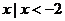 } B.{
} B.{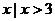 }
} 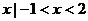 } D. {
} D. {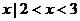 }
}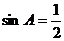 ”是“
”是“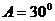 ”的
”的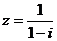 的共轭复数是
的共轭复数是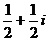 B.
B.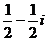 C.
C.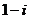 D.
D. 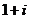
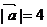 和
和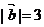 ,
,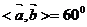 ,则
,则 的值为
的值为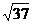 D.
D.
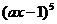 的展开式中
的展开式中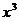 的系数是80,则实数
的系数是80,则实数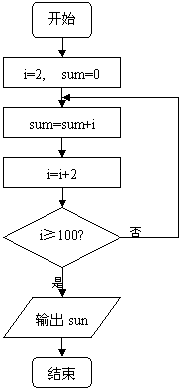 A.-2 B.
A.-2 B.
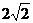 C.
C. 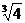 D. 2
D. 2 A.2450 B. 2550
A.2450 B. 2550  的定义域是 ,单调递减区间是 。
的定义域是 ,单调递减区间是 。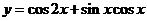 的最小正周期
的最小正周期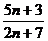 ,则这两个数列的第9项之比是 。
,则这两个数列的第9项之比是 。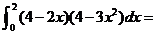 。
。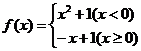 ,若
,若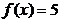 ,则
,则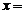 。
。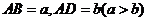 ,沿对角线AC 将△
,沿对角线AC 将△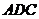 折起,使
折起,使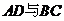 垂直,则异面直线
垂直,则异面直线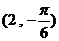 到直线:
到直线: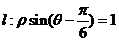 的距离是 .
的距离是 .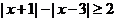 的解是 。
的解是 。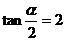 ,求
,求 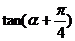 的值; (2)
的值; (2)
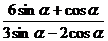 的值.
的值.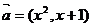 ,
,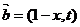 ,若函数
,若函数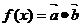 在区间
在区间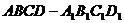 中,
中,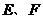 分别是
分别是
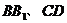 的中点.
的中点.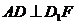 ;
;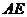 与
与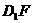 所成的角;
所成的角;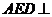 面
面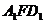
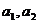 是正实数,则有
是正实数,则有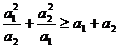 ;
; 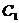 的方程为
的方程为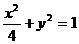 ,双曲线
,双曲线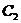 的左、右焦点分别是
的左、右焦点分别是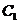 的左、右顶点,
的左、右顶点,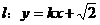 与双曲线
与双曲线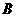 ,且
,且