天津精通高考复读学校数学教研组组长 么世涛
一、选择题 :1-4, BBBB ;5-8,DABD。
提示:1.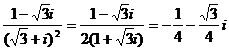
2.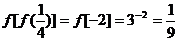
3.用 代替
代替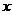 得
得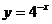
4.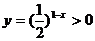
5.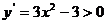 ,
,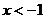 或
或
6.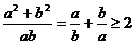
7.略
8.
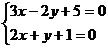
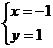
二、填空题:9.60; 10. 15:10:20 ; 11.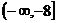 ; 12.
; 12.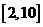 ;
;
13.0.74 ; 14. ①、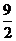 ;②、圆;③.
;②、圆;③.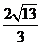
提示:
9.
10. ,
, ,
,
11.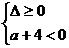 ,
,
12. ,
, ,
,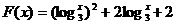 ,
,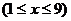
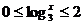 ,
,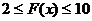
13.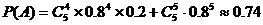
14.略
三、解答题
15. 解:(1)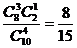 .
.
(2)设抽取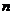 件产品作检验,则
件产品作检验,则 ,
,
 ,得:
,得: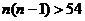 ,即
,即 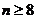
故至少应抽取8件产品才能满足题意.
16. 解:由题意得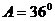 ,
,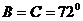 ,原式可化为
,原式可化为 ,
,
而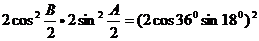
 ,
,
故原式=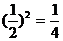 .
.
17. 解:(1)显然 ,连接
,连接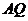 ,∵
,∵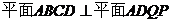 ,
,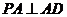 ,
,
∴ .由已知
.由已知 ,∴
,∴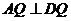 ,
,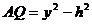 .
.
∵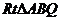 ∽
∽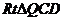 ,
,  ,
,
∴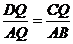 即
即 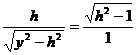 .
.
∴ .
.
(2) 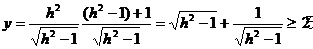
当且仅当 时,等号成立.此时
时,等号成立.此时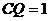 ,即
,即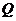 为
为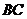 的中点.于是由
的中点.于是由 ,知平面
,知平面 ,
,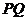 是其交线,则过
是其交线,则过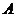 作
作
 。
。
∴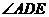 就是
就是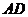 与平面
与平面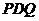 所成的角.由已知得
所成的角.由已知得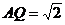 ,
, ,
,
∴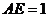 ,
, 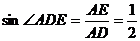 ,
, 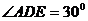 .
.
(3) 设三棱锥 的内切球半径为
的内切球半径为 ,则
,则

∵ ,
, ,
,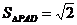 ,
, ,
, ,
,
∴ .
.
18. 解: (1) 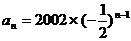 ,
,
(2) ∵  ,
,
∴当 时,
时,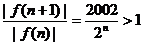

∴当 时,
时,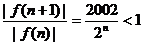 ,
,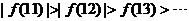
∵ ,
,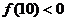 ,
, ,
, .
.
∴ 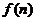 的最大值为
的最大值为 或
或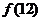 中的最大者.
中的最大者.
∵ 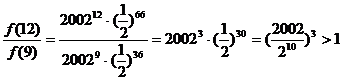
∴ 当 时,
时,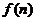 有最大值为
有最大值为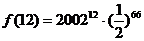
 .
.
19.(1)解:∵函数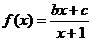 的图象过原点,
的图象过原点,
∴ 即
即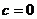 ,
,
∴ .
.
又函数 的图象关于点
的图象关于点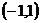 成中心对称,
成中心对称,
∴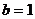 ,
,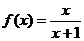 .
.
(2)解:由题意有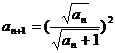 即
即 ,
,
即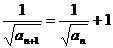 ,即
,即 .
.
∴数列{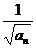 }是以1为首项,1为公差的等差数列.
}是以1为首项,1为公差的等差数列.
∴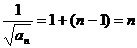 ,即
,即 . ∴
. ∴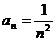 .
.
∴ 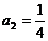 ,
,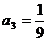 ,
, ,
,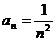 .
.
(3)证明:当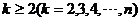 时,
时,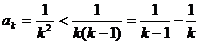
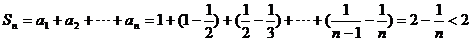
故 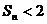
20. (1)解:∵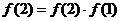 ,又
,又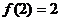 ,
,
∴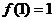 .
又∵
.
又∵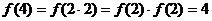
 ,且
,且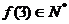
∴ 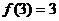 .
.
(2)解:由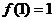 ,
,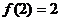 ,
,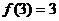 猜想
猜想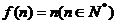
(3)证明:用数学归纳法证明:
①当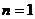 时,
时,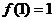 ,猜想正确;
,猜想正确;
②假设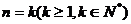 时,猜想正确,即
时,猜想正确,即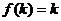
1°若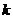 为正奇数,则
为正奇数,则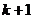 为正偶数,
为正偶数, 为正整数,
为正整数,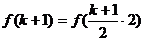
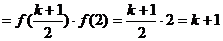
2°若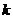 为正偶数,则
为正偶数,则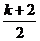 为正整数,
为正整数,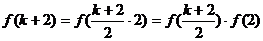
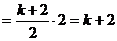 ,又
,又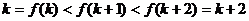 ,且
,且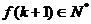
所以
即当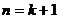 时,猜想也正确
时,猜想也正确
由①,②可知,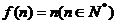 成立.
成立.
(二)
一、1-4,AABB,5-8,CDCB;
提示: 1.  即
即 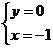
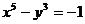
2. 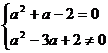 即
即 
3. 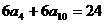 即
即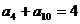 ,也就是
,也就是 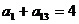 ,
,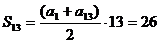
4.先确定是哪两个人的编号与座位号一致,有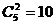 种情况,如编号为1的人坐1号座位,且编号为2的人坐2号座位有以下情形:
种情况,如编号为1的人坐1号座位,且编号为2的人坐2号座位有以下情形:
|
人的编号 1 2 3 4 5 座位号 1 2 5 3 4 人的编号 1 2 3 4 5 座位号 1 2 4 5 3
所以,符合条件的共有10×2=20种。 5. 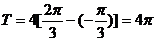 ,又 ,又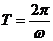 ,所以 ,所以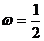 又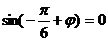 ,且 ,且 ,所以 ,所以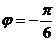 6.略 7.略 8. 密文shxc中的s对应的数字为19,按照变换公式: 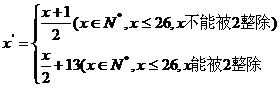 ,原文对应的数字是12,对应的字母是 ,原文对应的数字是12,对应的字母是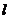 ; ;
密文shxc中的h对应的数字为8,按照变换公式: 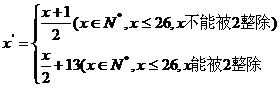 ,原文对应的数字是15,对应的字母是 ,原文对应的数字是15,对应的字母是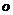 ; ;
二、9.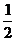 ; 10.2;11.-48; 12. ; 10.2;11.-48; 12. 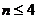 ; 13、5; 14、①3,② ; 13、5; 14、①3,②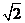 ,③ ,③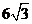 提示: 9.
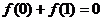 , , , ,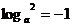 10. 数列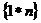 是首相为 是首相为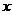 ,公差为 ,公差为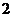 的等差数列,于是 的等差数列,于是 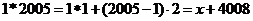 又 又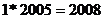 ,所以 ,所以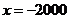
11. 特殊值法。取通径,则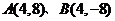 , , , ,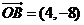 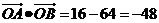 。 。
12.因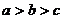 , ,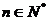 ,所以 ,所以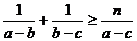 同解于 同解于 又 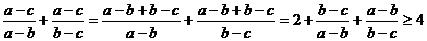 所以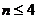 。 。 13.略 。 。
14、(1)如图:∵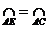 ∴∠1=∠2=∠3=∠P+∠PFD
=∠FEO+∠EFO ∴∠FEO=∠P,可证△OEF∽△DPF 即有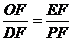 ,又根据相交弦定理DF・EF=BF・AF ,又根据相交弦定理DF・EF=BF・AF 可推出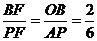 ,从而 ,从而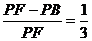 ∴PF=3 (2) ∵PF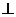 QF, ∴ QF, ∴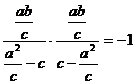 ∴ ∴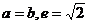 (3)略。 三、15.解:(1) 依题知,得 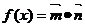 
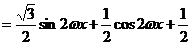

 又 又  所以 所以 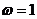
(2) 由(1)得
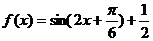 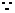 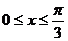
∴ 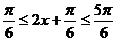 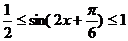 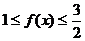 故 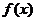 的值域为 的值域为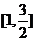 。 。 16.解:设飞机A能安全飞行的概率为 ,飞机B能安全飞行的概率为 ,飞机B能安全飞行的概率为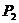 ,则 ,则 
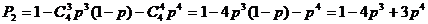

又 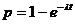 所以 所以 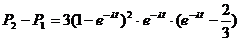 当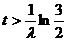 时, 时,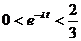 , , , , ; ; 当 时, 时,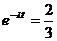 , , , ,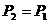 ; ; 当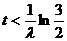 时, 时,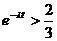 , ,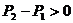 , , ; ; 故当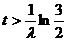 时,飞机A安全;当 时,飞机A安全;当 时,飞机A与飞机B一样安全;当 时,飞机A与飞机B一样安全;当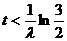 时,飞机B安全。 时,飞机B安全。 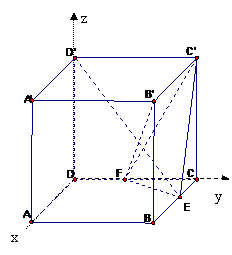
17.(1) 证明:以D为坐标原点,DA所在的直线x 轴,建立空间直角坐标系如图。 设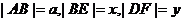 ,则 ,则 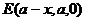 , ,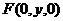 , ,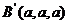 , ,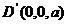
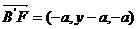 , ,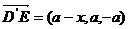
又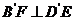 ,所以 ,所以 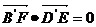
即 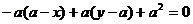 ,也就是 ,也就是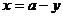 又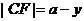 ,所以 ,所以 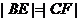 ,即 ,即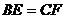 。 。 (2)解:方法1、找出二面角,再计算。 方法2、由(1)得: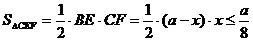 (当且仅当 (当且仅当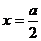 取等号) 取等号) 即 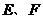 分别为 分别为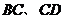 的中点,于是 的中点,于是 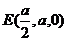 , ,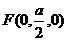 。 。 又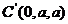 ,所以 ,所以 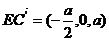 , ,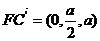 设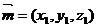 是平面 是平面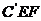 的一个法向量,则 的一个法向量,则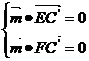 即 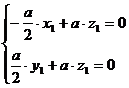 也就是 也就是 取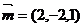 易知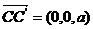 是平面 是平面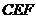 的一个法向量, 的一个法向量, 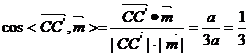
18.(1) 证明:依题知得: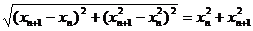 整理,得 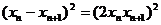 又 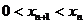 所以 所以 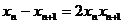 即 即 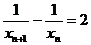 故 数列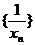 是等差数列。 是等差数列。 (2) 由(1)得  即 即 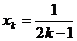 ( (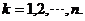 ) ) 又 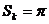 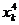 所以 所以 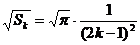 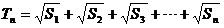
=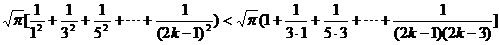 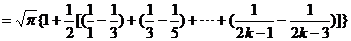
=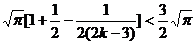 故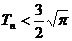 19.解:(1) 依题知得  欲使函数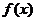 在 在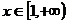 是增函数,仅须 是增函数,仅须 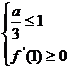 或 或
关闭

| | |