1. 已知集合 A = {x | x 2 + 2ax + 1 = 0} 的真子集只有一个,则 a 值的集合是( )
A.(-1,1) B. (-¥,-1]∪[1,+¥) C. {-1,1} D.{0}
2.函数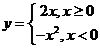 的反函数是( )
的反函数是( )
A.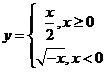 B.
B.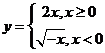 C.
C.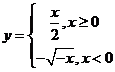
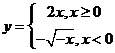
3.复数 的虚部为( )
的虚部为( )
A.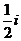 B.
B.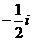 C.
C.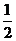 D.
D.
4.设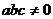 ,“
,“ ”是“曲线
”是“曲线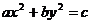 为椭圆”的( )
为椭圆”的( )
A.充分非必要条件 B.必要非充分条件 C.充分必要条件 D.既非充分又非必要条件
5.曲线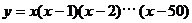 在原点处的切线方程为( )
在原点处的切线方程为( )
A.y = 1275x B.y = 502x C.y = 100x D.y = 50!x
 6.给出平面区域如图所示,若使目标函数
6.给出平面区域如图所示,若使目标函数 取得最大值的最优解有无穷多个,则
取得最大值的最优解有无穷多个,则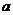 的值为( )
的值为( )
A.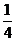 B.
B.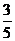
C.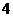 D.
D.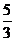
7.已知双曲线的离心率e=2,且与椭圆 有相同的焦点,该双曲线的渐近线方程是( )
有相同的焦点,该双曲线的渐近线方程是( )
A.  B.
B.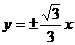 C.
C.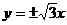 D.
D.
8.已知ΔABC的三个顶点A、B、C及所在平面内一点P满足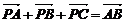 ,则点P与ΔABC的关系是:
( )
,则点P与ΔABC的关系是:
( )
A、P在ΔABC内部 B、P在ΔABC外部
C、P在直线AB上 D、P在ΔABC的AC边的一个三等分点上
9.在线段[0,1]上任意投三个点,问由0至三点的三线段,能构成三角形与不能构成三角形这两个事件中哪一个事件的概率大。( )
A.一样大 B.能够成三角形概率大 C.不能够成三角形概率大 D.无法比较
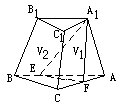 10.如图(1),正三棱台
10.如图(1),正三棱台 的上、下底面积之比为1:9,过
的上、下底面积之比为1:9,过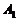 作平行于侧面
作平行于侧面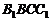 的截面
的截面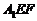 ,将棱台分成两个多面体,
,将棱台分成两个多面体,
则这两部分体积之比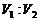 等于( )
等于( )
A.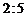 B.
B.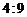 C.
C.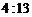 D.
D.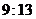
图(1)
11.若关于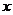 的不等式组
的不等式组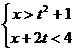 的解集不是空集,则实数
的解集不是空集,则实数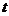 的取值不可能是( )
的取值不可能是( )
A.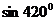 B.
B.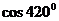 C.
C. D.
D.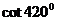
12.函数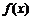 的图象为C,且
的图象为C,且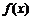 有反函数,则将C( )
有反函数,则将C( )
A.向右向下各平移一个单位长度
B.向右向上各平移一个单位长度
C.向左向下各平移一个单位长度
D.向左向上各平移一个单位长度
后,再作关于直线y=x对称的图象,即为函数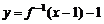 的图象。
的图象。
13.如图(2),该程序运行后输出的结果为 .

图(2)
14. 对于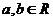 ,若
,若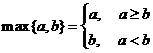 ,则函数
,则函数
 的最小值为__________.
的最小值为__________.
15. 23.观察: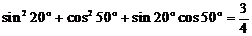 ,
,
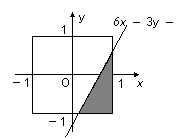
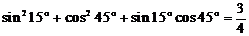
写出一个与以上规律相同的等式:_______________
16. 向图中所示的正方形随机投掷飞镖,则飞镖落在阴影部分的概率为 。
17.△ABC的三边为a,b,c,已知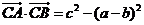 ,且
,且
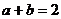 ,求
,求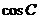 的值及三角形面积
的值及三角形面积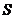 的最大值.
的最大值.
18.已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,
∠ADB=60°,E、F分别是AC、AD上的动点,且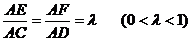
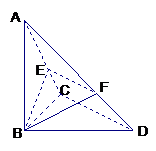 (Ⅰ)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(Ⅰ)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(Ⅱ)当λ为何值时,平面BEF⊥平面ACD? (14分)
19.如图所示是某班学生一次数学考试成绩的频率分布直方图,
其中纵轴表示学生数,观察图形,回答下列问题:
(1)全班有多少学生; (2)此次考试平均成绩大概是多少;
(3)不及格的人数有多少?占全班多大比例?
(4)如果80分以上的成绩为优良, 那么这个班的优良率为多少?
 |
学生数
14
13
12
11
10
9
8
7
6
5
4
3
2
1
29 39 49 59 69 79 89 99 成绩
20.已知函数
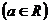
(1)若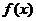 在
在 上是减函数,求
上是减函数,求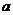 的最大值;
的最大值;
(2)若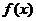 的单调递减区间是
的单调递减区间是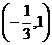 ,求函数y=
,求函数y=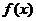 图像过点
图像过点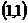 的切线与两坐标轴围成图形的面积。
的切线与两坐标轴围成图形的面积。
。
21. 已知数列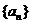 满足
满足 且对一切
且对一切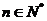 有
有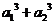 +……
+……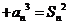 ,
,
(1)求证:对一切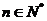 有
有
(2)求数列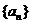 的通项公式
的通项公式
(3)求证: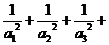 ……
……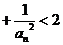
22. 已知椭圆E: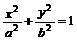 (a>b>0),以F1(-c,0)为圆心,以a-c为半径作圆F1,过点B2(0,b)作圆F1的两条切线,设切点为M、N.
(a>b>0),以F1(-c,0)为圆心,以a-c为半径作圆F1,过点B2(0,b)作圆F1的两条切线,设切点为M、N.
(1)若过两个切点M、N的直线恰好经过点B1(0,-b)时,求此椭圆的离心率;
(2)若直线MN的斜率为-1,且原点到直线MN的距离为4(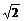 -1),求此时的椭圆方程;
-1),求此时的椭圆方程;
(3)是否存在椭圆E,使得直线MN的斜率k在区间(- )内取值?若存在,求出椭圆E的离心率e的取值范围;若不存在,请说明理由.
)内取值?若存在,求出椭圆E的离心率e的取值范围;若不存在,请说明理由.
参 考 答 案
第Ⅰ卷
题目
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
C
D
B
D
B
C
D
A
B
C
D
13.63
14.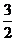
15. 
16. 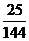
解: 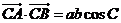 ,又由余弦定理得
,又由余弦定理得
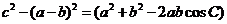
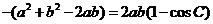 .
.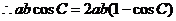 ,
,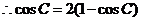 ,得
,得 ,
,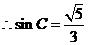 .又
.又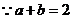 ,
,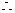
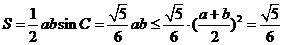 .
.
当且仅当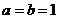 时,等号成立.
时,等号成立.
 .
.
18.本题满分12分
证明:(Ⅰ)∵AB⊥平面BCD, ∴AB⊥CD,
∵CD⊥BC且AB∩BC=B, ∴CD⊥平面ABC. 2分
又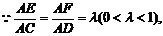
∴不论λ为何值,恒有EF∥CD,∴EF⊥平面ABC,EF 平面BEF,
平面BEF,
∴不论λ为何值恒有平面BEF⊥平面ABC. 6分
(Ⅱ)由(Ⅰ)知,BE⊥EF,又平面BEF⊥平面ACD,
∴BE⊥平面ACD,∴BE⊥AC. 8分
∵BC=CD=1,∠BCD=90°,∠ADB=60°,
∴ 10分
10分
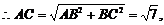 由AB2=AE・AC 得
由AB2=AE・AC 得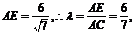 12分
12分
故当 时,平面BEF⊥平面ACD.
时,平面BEF⊥平面ACD.
19. 本题满分12分
解:(1)1+2+3+6+8+10+14=44
(2) 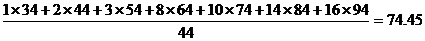
(3)不及格的人数有6人,占全班比例是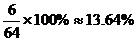
(4)优良率是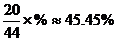
20. 本题满分12分
解析:解:(1)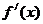 =
=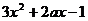 ,由题意可知,
,由题意可知,
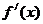 在(0,1)上恒有
在(0,1)上恒有
则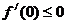 且
且 ,得
,得 ,
,
所以a的最大值为 -1
(2)
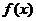 的单调递减区间是
的单调递减区间是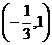 ,
,
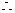
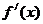 =
=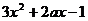 =0的两个根为
=0的两个根为 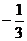 和1,
和1,
可求得a= -1,
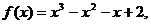
①
若(1,1)不是切点,则设切线的切点为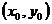 ,
,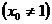 ,
,
则有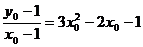
 , 解得
, 解得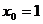 (舍),
(舍),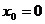 ,
,
 ,k= -1
,k= -1
②
若(1,1)是切点,则k=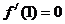
综上,切线方程为y=1,x+y-2=0
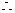 这两条切线方程与两坐标轴围成的图形为直角梯形
这两条切线方程与两坐标轴围成的图形为直角梯形
它的面积S=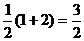 …………………………………………………
…………………………………………………
21. 本题满分12分
解:(1)由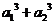 +……
+……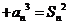 得
得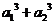 +……+
+……+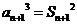
相减得:
 ・
・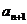
(2)由(1)知 得
得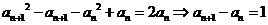 (
( ≥2)
≥2)
又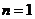 时
时 ,由
,由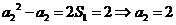
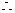
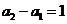
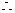
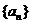 为等差数列且
为等差数列且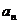 =
=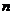
(3)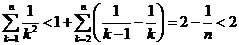
22. 解:(1)圆F1的方程是(x+c)2+y2=(a-c)2,因为B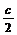 )2+(y-
)2+(y- )2=
)2=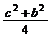 ,从而两个圆的公共弦MN的方程为cx+by+c2=(a-c)2,又点B1在MN上,
,从而两个圆的公共弦MN的方程为cx+by+c2=(a-c)2,又点B1在MN上,
∴a2+b2
∴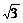 -1.(负值已舍去)
-1.(负值已舍去)
(2)由(1)知,MN的方程为cx+by+c2=(a-c)2,由已知- =-1.
=-1.
∴b=c,而原点到MN的距离为d=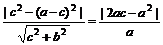 =|
=|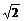 a,
a,
∴a=4,b2=c2=8,所求椭圆方程是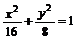 ;
;
(3)假设这样的椭圆存在,由(2)则有- <-
<- <-
<- ,
,
∴ <
< <
< ,∴
,∴ <
<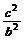 <
<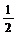 ,∴
,∴ <
<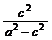 <
<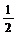 .故得2<
.故得2<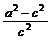 <3,
<3,
∴3<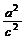 <4,求得
<4,求得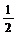 <e<
<e< ,即当离心率取值范围是(
,即当离心率取值范围是(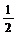 ,
, )时,直线MN的斜率可以在区间?(
)时,直线MN的斜率可以在区间?( ,-
,- )内取值.
)内取值.

