1.定义集合运算: 设集合
设集合 ,
,
 ,则集合
,则集合 的所有元素之和为( )
的所有元素之和为( )
A.1
B.
2.复数 ,则
,则 的值为( )
的值为( )
A.0
B.-
3.设集合 ,那么“
,那么“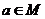 ”是“
”是“ ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
 C.充分必要条件
D.既不充分也不必要条件
C.充分必要条件
D.既不充分也不必要条件
4.某赛季甲、乙两名篮球运动员每场比赛
得分的径叶图如图,则以下说法正确的
是( )
A.甲总体得分比乙好,且甲比乙稳定;
B.甲总体得分比乙好,但乙比甲稳定;
C.乙总体得分比甲好,且乙比甲 稳定;
D. 乙总体得分比甲好,但甲比乙稳定。
 |
5.如图所示为一个简单几何体的三视图,则其对应的实物是( )
6.已知椭圆 ,
, 是其右焦点,过
是其右焦点,过 作椭圆的弦
作椭圆的弦 ,设
,设 ,则
,则 的值为( )
的值为( )
A. B.
B.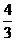 C.
C. D.
D.
7.定义两种运算: ,则函数
,则函数 为( )
为( )
A.奇函数 B.偶函数 C.奇函数且为偶函数 D.非奇函数且非偶函数
8.已知向 ,若
,若 ,则
,则 与
与 的夹角为( )
的夹角为( )
A.30° B.60° C.120° D.150°
9.右图是计算1+2+3+…+100的一个程序框图,则条件框内是( )
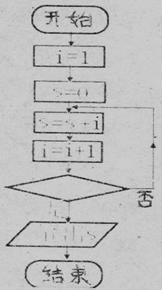 A.
A. B.
B. C.
C. D.
D.
10.若过点 的直线
的直线 与曲线
与曲线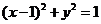 有公共点,则
有公共点,则
直线 斜率的取值范围为( )
斜率的取值范围为( )
A. B.
B.
C. D.
D.
11.如图,椭圆中心在坐标原点, 为左焦点,当
为左焦点,当 时,
时,
其离心率为 ,此类椭圆被称为“黄金椭圆”类比“黄金
,此类椭圆被称为“黄金椭圆”类比“黄金
 椭圆”,可推算出“黄金双典线”的离心率
椭圆”,可推算出“黄金双典线”的离心率 等于( )
等于( )
A. B.
B. C.
C. D.
D.
12.已知 且
且 ,
, ,当
,当 时均有
时均有 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A. B.
B. C.
C. D.
D.
13.在平面直角坐标系 中,设
中,设 是横坐标与纵坐标的绝对值均不大于4的点构成的区域
是横坐标与纵坐标的绝对值均不大于4的点构成的区域 是到原点的距离不大于1的点构成的区域,向
是到原点的距离不大于1的点构成的区域,向 中随机投一点,
中随机投一点,
则落入 中的概率为____________________
中的概率为____________________
14.若 且
且 ,函数
,函数 与
与 的图象有两个交点,则
的图象有两个交点,则 的取值范围是___.
的取值范围是___.
15.如果实数 ,b满足条件:
,b满足条件: 则
则 的最小值是________________。
的最小值是________________。
16.下列四个命题:
①圆 与直线
与直线 相交,所得弦长为2;
相交,所得弦长为2;
②直线 与圆
与圆 恒有公共点;
恒有公共点;
③若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为 ;
;
④若棱长为 的正四面体的顶点都在同一球面上,则该球的体积为
的正四面体的顶点都在同一球面上,则该球的体积为 。
。
其中,正确命题的序号为________________(写出所有正确命题的序号)。
17.(本小题满分12分)
在平面直角坐标系下,已知 ,
, ,
, ,
,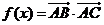 。
。
(Ⅰ)求 的表达式;
的表达式;
(Ⅱ)求 的最小正周期和值域。
的最小正周期和值域。
18.(本小题满分12分)
已知函数 。
。
(1)若 从集合
从集合 中任取一个元素,
中任取一个元素, 从集合
从集合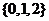 中任取一个元素,
中任取一个元素,
求方程 有两个不相等实根的概率;
有两个不相等实根的概率;
(2)若 从区间
从区间 中任取一个数,
中任取一个数, 从区间
从区间 中任取一个数,求方程
中任取一个数,求方程 没有实根的概率。
没有实根的概率。
19.(本小题满分12分)
如图1所示,正△ABC的边长为
(1)试判断翻折后直线AB与平面DEF的位置关系,并说明理由;
(2)求三棱锥C-DEF的体积。
20.(本小题满分12分)
已知数列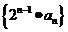 的前
的前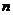 项和
项和
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前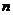 项和。
项和。
21.本小题满分12分)
已知动点 到双曲线
到双曲线 的两个焦点
的两个焦点 的距离之和为定值
的距离之和为定值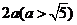 ,
,
且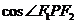 的最小值为
的最小值为 。
。
(1)求动点 的轨迹方程;
的轨迹方程;
(2)若已知点
 、
、 在动点
在动点 的轨迹上,且
的轨迹上,且 ,
,
求实数 的取值范围。
的取值范围。
22.(本小题满分14分)
已知函数 。
。
(Ⅰ)求 的值域;
的值域;
(Ⅱ)设 ,函数
,函数 。若对任意
。若对任意 ,总存在
,总存在 ,使
,使 ,求实数
,求实数 的取值范围。
的取值范围。


