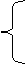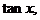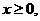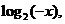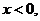1. 已知集合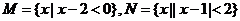 ,则
,则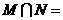 ( )
( )
A. 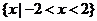 B.
B. 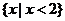

C. 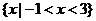 D.
D. 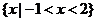

2. 已知函数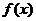 =
则
=
则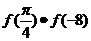 =( )
=( )
A. 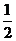 B. -
B. -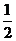 C. 3 D. -3
C. 3 D. -3
3. 若向量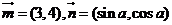 ,且
,且 ∥
∥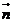 ,则
,则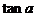 等于( )
等于( )
A.  B.
B.  C.
C. 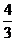 D.
D. 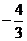

4. 若数列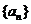 的前n项和
的前n项和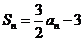 ,那么这个数列的通项公式是( )
,那么这个数列的通项公式是( )
A. 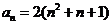 B.
B.
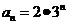

C. 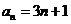 D.
D.
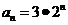

5. 函数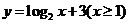 的反函数为( )
的反函数为( )
A. 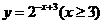 B.
B.
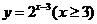

C. 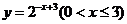 D.
D. 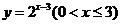

6. 在直二面角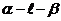 中,直线
中,直线 ,直线
,直线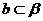 ,a、b与
,a、b与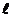 相交但不垂直,则( )
相交但不垂直,则( )
A. a和b不可能垂直,但可能平行 B. a和b可能垂直,但不可能平行
C. a和b可能垂直,也可能平行 D. a和b不可能垂直,也不可能平行
7. 已知向量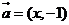 ,
,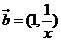 则不等式
则不等式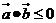 的解集为( )
的解集为( )
A. 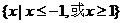 B.
B. 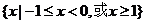

C. 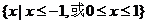 D.
D. 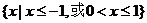

8. 已知△ABC的三个顶点在同一球面上,∠BAC=900,AB=AC=2,若球心O到平面ABC的距离为1,则该球的表面积为( )
A.  B.
B. 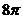 C.
C. 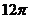 D.
D. 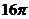

9. 已知抛物线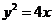 的准线与双曲线
的准线与双曲线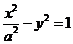 相交于A、B两点,F为抛物线的焦点,若△FAB为直角三角形,则双曲线的离心率是( )
相交于A、B两点,F为抛物线的焦点,若△FAB为直角三角形,则双曲线的离心率是( )
A. 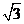 B.
B. 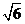 C. 2 D. 3
C. 2 D. 3
10. 在一块形状为直角三角形的土地上划出一块矩形土地建造游泳池(如图中阴影所示),则这块矩形土地的最大面积是( )
A. 
C. 
4
1
2
3
5
11. 编号为A、B、C、D、E的五个小球放在如图所示的五个盒子中,每个盒子只能放1个小球,要求A不能放在1、2号,B必须放在与A相邻的盒子中,则不同的放法有( )
A. 30种 B. 32种 C. 36种 D. 42种
12. 已知函数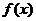 是以2为周期的偶函数,当
是以2为周期的偶函数,当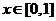 时
时 ,那么在区间
,那么在区间
[-1,3]内,关于x的方程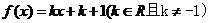 的根的个数( )
的根的个数( )
A. 不可能有三个
B. 最少有一个,最多有四个
C. 最少有一个,最多有三个 D. 最少有两个,最多有四个
第Ⅱ卷(非选择题,共90分)
13. 某校有教师200名,男生1200名,女生1000名,现用分层抽样方法从所有师生中抽取一个容量为n的样本,已知女生中抽取的人数为80,则n=
.
14. 在 的展开式中含
的展开式中含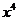 的项的系数是
.
的项的系数是
.
15. 已知函数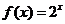 ,等差数列
,等差数列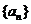 的公差为2,若
的公差为2,若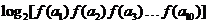
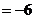 ,则
,则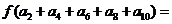 .
.
16. 已知函数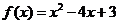 ,集合
,集合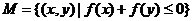 ,集合
,集合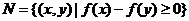 ,则集合
,则集合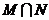 的面积是
.
的面积是
.
17. (本小题满分10分)在△ABC中,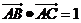 ,
,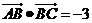

(1)求AB边的长度;
(2)求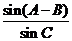 的值.
的值.
 18. (本小题满分12分)等比数列
18. (本小题满分12分)等比数列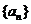 同时满足下列两个条件:1
同时满足下列两个条件:1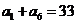 ;2
;2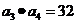 ,试求数列
,试求数列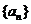 的通项公式和前n项和
的通项公式和前n项和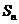 .
.
19. (本小题满分12分)甲、乙2人各进行1次射击,如果2人击中目标的概率都是0.6,计算:
(1)2人都击中目标的概率;
(2)其中恰有1人击中目标的概率;
(3)至少有1人击中目标的概率.
20. (本小题满分12分)如图所示,已知正四棱柱ABCD-A1B
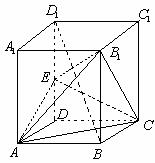 (1)求截面EAC的面积;
(1)求截面EAC的面积;
(2)求异面直线A1B1与AC之间的距离;
(3)求三棱锥B1-EAC的体积.
21. (本小题满分12分)已知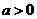 ,函数
,函数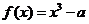 ,
,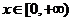 设
设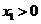 ,记曲线
,记曲线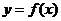 在点M(
在点M(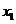 ,
,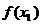 )处的切线为
)处的切线为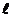 .
.
(1)求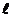 的方程;
的方程;
(2)设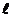 与x轴的交点为(x2,0),证明:1
与x轴的交点为(x2,0),证明:1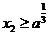 ;2若
;2若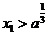 ,则
,则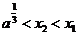 .
.
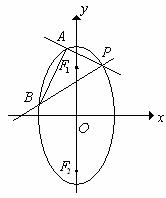 22. (本小题满分12分)已知椭圆
22. (本小题满分12分)已知椭圆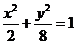 两焦点分别为F1、F2、P是椭圆在第一象限弧上一点,并满足
两焦点分别为F1、F2、P是椭圆在第一象限弧上一点,并满足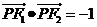 ,过P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点.
,过P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点.
(1)求P点坐标;
(2)求证直线AB的斜率k为定值;
(3)求△PAB面积的最大值.