A. a和b不可能垂直,但可能平行 B. a和b可能垂直,但不可能平行
- 答案
一、DCABB DDCBC AB
二、13.
192 14. ―640
15. 4 16. 
17.
(1)
 …5分
…5分
(2)由已知及(1)知 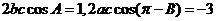

 由
由 正弦定理得:
正弦定理得:
 ……………………10分
……………………10分
18.由题设及等比数列的性质得  ①
①
又 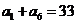 ②
②
由①②得 或
或  …………………4分
…………………4分
 或
或  …………………6分
…………………6分
 或
或 …………………8分
…………………8分
当 时,
时, …………………10分
…………………10分
当 时,
时, ………………12分
………………12分
19.略(见课本B 例1)
例1)
20.解:
(1)在正四棱柱 中,因为
中,因为

所以
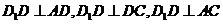
又 
连接 交
交 于点
于点 ,连接
,连接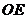 ,则
,则 ,所以
,所以

所以 是由截面
是由截面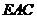 与底面
与底面 所成二面角的平面角,即
所成二面角的平面角,即



所以  .....................4分
.....................4分
(2)由题设知 是正四棱柱.
是正四棱柱.
因为

所以

又

所以 是异面直线
是异面直线 与
与 之间的距离。
之间的距离。
因为 ,而
,而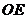 是截面
是截面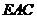 与平面
与平面 的交线,
的交线,
所以


即异面直线 与
与 之间的距离为
之间的距离为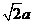
(3)由题知
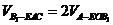
因为
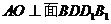
所以 是三棱锥
是三棱锥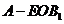 的高,
的高,
在正方形 中,
中, 分别是
分别是 的中点,则
的中点,则

所以

即三棱锥 的体积是
的体积是 .
.
21.(1)解: ,由此得切线
,由此得切线 的方程为
的方程为
 ………………………4分
………………………4分
(2)切线方程令 ,得
,得
①
 当且仅当
当且仅当 时等号成立。………………………9分
时等号成立。………………………9分
②若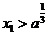 ,则
,则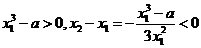 又由
又由
 ………………………12分
………………………12分
22.(1)由题可得 ,设
,设




又 又
又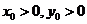

 点P的坐标为
点P的坐标为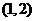 ……………………3分
……………………3分
(2)由题意知,量直线的斜率必存在,设PB的斜率为
则PB的直线方程为 :由
:由 得
得
 ,显然1是该方程的根
,显然1是该方程的根
 ,依题意设
,依题意设 故可得A点的横坐标
故可得A点的横坐标



 ……………………7分
……………………7分
(3)设AB的方程为 ,带入
,带入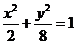 并整理得
并整理得


 …………………(
…………………( )
)
设

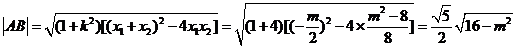
点P到直线AB的距离

当且仅当 ,即
,即 时取“=”号(满足条件
时取“=”号(满足条件 )
)
故 的面积的最大值为2
………………………12分
的面积的最大值为2
………………………12分

