1、已知复数 则
则 ______________。
______________。
2、(理) 的展开式中第三项的系数为______________。
的展开式中第三项的系数为______________。
(文)方程 的解是______________。
的解是______________。
3、若 ,则
,则 的值是 _______.
的值是 _______.
4、已知两点 ,点P满足
,点P满足 ,则点P的轨迹方程为__________________________。
,则点P的轨迹方程为__________________________。
5、李老师家藏有一套精装的四卷的《西游记》,任意排放在书架的同一层上,则卷序自左向右或自右向左恰为 的概率是_________________。
的概率是_________________。
6、已知函数 的反函数的图象经过点(4,2),则
的反函数的图象经过点(4,2),则 的值是____________.。
的值是____________.。
7、(理)已知直线 的极坐标方程为
的极坐标方程为 ,则点
,则点 到直线
到直线 的距离为__________________。
的距离为__________________。
(文)若满足不等式组 ,则目标函数
,则目标函数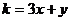 的最大值为 ___。
的最大值为 ___。
8、将一张画了直角坐标系且两轴的长度单位相同的纸折叠一次,使点(2,0)与点(-2,4)重合,若点(5,8)与点(m,7)重合,则n的值为________________________.
9、不等式 对一切非零实数x总成立 , 则
对一切非零实数x总成立 , 则 的取值范围是 _______。
的取值范围是 _______。
10、若定义在区间 内的函数
内的函数 满足
满足 ,则实数
,则实数 的取值
的取值
范围是___________________。
11、为说明“已知 ,对于一切
,对于一切 那么
那么 。”
。”
是假命题,试举一反例为
12、若 ,定义
,定义 ,则
,则 的值为____________
的值为____________
13、在下列关于直线l、m与平面α、β的命题中,真命题是 ( )
(A)若l β,且α⊥β,则l⊥α. (B)若l⊥β,且α∥β,则l⊥α.
β,且α⊥β,则l⊥α. (B)若l⊥β,且α∥β,则l⊥α.
(C)若α∩β=m,且l∥m,则l∥α (D)若l⊥β,且α⊥β,则l∥α.
14、等差数列{ }的前
}的前 项和记为
项和记为 ,若
,若 为一个确定的常数,则下列各数中可以用这个常数表示的是( )
为一个确定的常数,则下列各数中可以用这个常数表示的是( )
(A) (B)
(B) (C)
(C) (D)
(D)
 15、已知函数f (x)(0 ≤
x ≤1)的图象的一段圆弧(如图所示),若
15、已知函数f (x)(0 ≤
x ≤1)的图象的一段圆弧(如图所示),若 ,则( )
,则( )
(A) (B)
(B)
(C) (D)前三个判断都不正确
(D)前三个判断都不正确
16、已知函数 满足
满足 对
对 恒成立,则( )
恒成立,则( )
(A)函数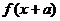 一定是偶函数 (B)函数
一定是偶函数 (B)函数 一定是偶函数
一定是偶函数
(C)函数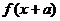 一定是奇函数 (D)函数
一定是奇函数 (D)函数 一定是奇函数
一定是奇函数
17、(12分)在锐角 中,
中, 是角
是角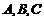 所对的边,
所对的边, 是该三角形的面积,若
是该三角形的面积,若
 。(1)求角
。(1)求角 的度数;(2)若
的度数;(2)若 ,求
,求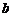 的值。
的值。
18、(12分)如图为某一几何体的展开图,其中 是边长为6的正方形,
是边长为6的正方形, ,
, ,
,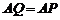 ,点
,点 、
、 、
、 、
、 及
及 、
、 、
、 、
、 共线.
共线.
(1)
沿图中虚线将它们折叠起来,使 、
、 、
、 、
、 四点重合,请画出其直观图,
四点重合,请画出其直观图,
(2)
试问需要几个这样的几何体才能拼成一个棱长为6的正方体 ?
?
19、(14分)已知抛物线 ,椭圆经过点
,椭圆经过点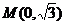 ,它们在
,它们在 轴上有共同焦点,椭圆的对称轴是坐标轴。
轴上有共同焦点,椭圆的对称轴是坐标轴。
(1)求椭圆的方程;
(2)若 是椭圆上的点,设
是椭圆上的点,设 的坐标为
的坐标为 (
( 是已知正实数),求
是已知正实数),求 与
与 之间的最短距离。
之间的最短距离。
20、(14分)在世博会后,昆明世博园作为一个旅游景点吸引四方宾客。按规定旅游收入
除上缴 的税收外,其余自负盈亏。目前世博园工作人员维持在400人,每天运
的税收外,其余自负盈亏。目前世博园工作人员维持在400人,每天运
营成本20万(不含工作人员工资),旅游人数 与人均消费额
与人均消费额 (元)的关系如下:
(元)的关系如下:

(1) 若游客在1000人到4000人之间,按人均消费额计算,求当天的旅游收入范围;
(2) 要使工作人员平均每人每天的工资不低于50元且维持每天正常运营(不负债),
每天的游客应不少于多少人?
21、(16分)对任意复数 ,定义
,定义 。
。
 (1) 若
(1) 若 ,求相应的复数
,求相应的复数 ;
;
(2)若 中的
中的 为常数,则令
为常数,则令 ,对任意
,对任意 ,是否一定有常数
,是否一定有常数 使得
使得 ?这样的
?这样的 是否唯一?说明理由。
是否唯一?说明理由。
(3)计算 ,并设立它们之间的一个等式。
,并设立它们之间的一个等式。
(理)由此发现一个一般的等式,并证明之。
22、(18分)已知函数
 ,函数
,函数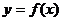 的图象与
的图象与 的图象关于点
的图象关于点 中心对称。
中心对称。
(1)求函数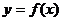 的解析式;
的解析式;
(2)如果 ,
, ,试求出使
,试求出使 成立的
成立的 取值范围;
取值范围;
(3)是否存在区间 ,使
,使 对于区间内的任意实数
对于区间内的任意实数 ,只要
,只要 ,且
,且 时,都有
时,都有 恒成立?
恒成立?


